
定常電流を学んでいきます。
ここはそこまで難しくないのでさらっと行きましょう。
電磁気界で有名なオームの法則が出てきます。
定常電流
まずは電流の強さが時間に依存しない定常電流から考えましょう。
定常電流では次の関係が成り立ちます。
導線を流れる電流を \(I_1\) 、その電流が2つに分岐したあとを \(I_2, I_3\) とするとこれらが等しくなるというものです。
$$I_1 = I_2+I_3$$
片方の辺にまとめると
$$0 = -I_1+I_2+I_3 $$
このようにゼロが出てきます。
これを一般化すると
$$\sum_i I_i = 0$$
になります。
つまり枝分かれする前とした後の電流の和は一定です。
電流密度
電流の定義から電流密度というものを考えてみます。
電流の正体は電荷の流れです。
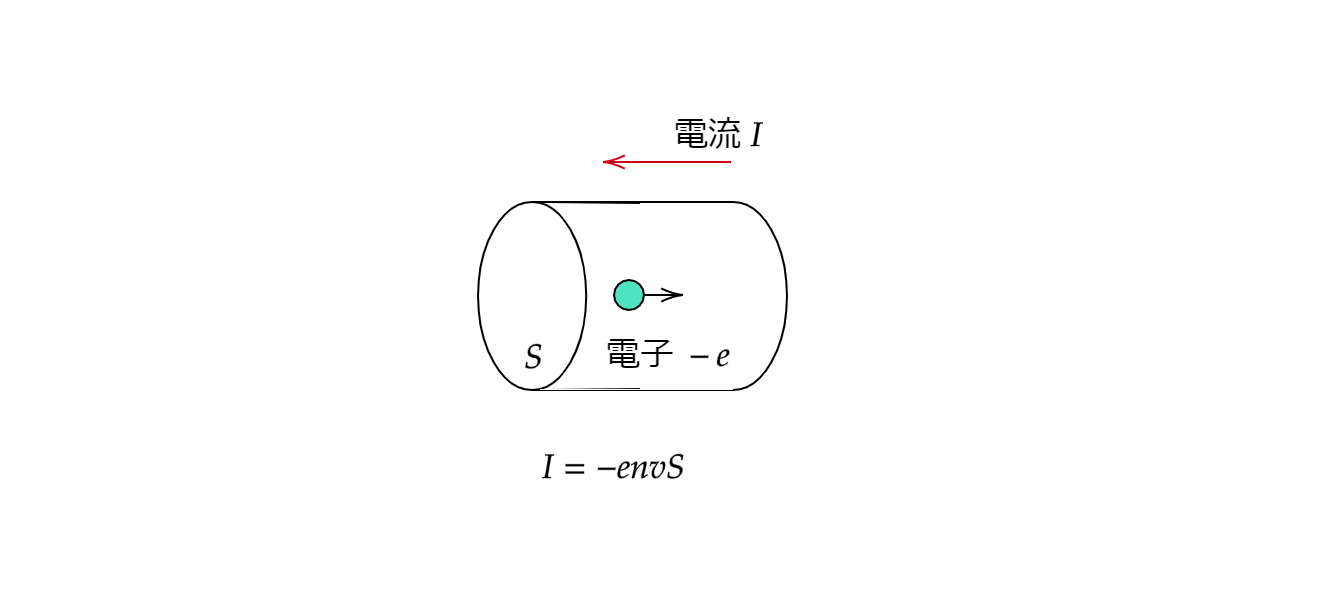
断面積が \(S\) の導体を通過する電荷 \(-e\) の速さを \(v\) とします。
また、導体の電流密度を \(n\) とすると電流は次のように表されます。
$$I = -envS$$
日本語で説明すると「単位時間当たりに断面積 \(S\) を通過する電子の数」が電流になります。
電流密度を \(i\) とするとこうなります。
$$i = -env$$
電流を断面積で割った値ですね。
ベクトル表記で表すと
$$\vec{i}(r) = -en\vec{v}(r)$$
です。
これからは電流密度が良く出てくるので覚えてください。
では、電流密度を使って、オームの法則を導いてみます。
オームの法則
オームの法則は有名ですね。
電流と抵抗の積が電位差になるという法則です。
$$I = \frac{\Delta \phi}{R}$$
\(I\) はもちろん電流です。 \(R\) は電気抵抗、 \(\Delta \phi\) は電位差です。
この電気抵抗は物質によって異なります。
物体の長さを \(l\) 、その物体の断面積を \(R\) 、物体の抵抗率を \(\rho\) とすると電気抵抗は
$$R = \rho\frac{l}{S}$$
となります。
電気抵抗は電気の通りにくさを示しますが、このままでは使いずらいこともあるので、その逆数を取った
$$\sigma = \frac{1}{\rho}$$
電気伝導度を使うことがあります。
ただ逆数を取ればよいだけなので簡単ですね。
この電気伝導度を使ってオームの法則を表してみましょう。
オームの法則は有名ですね。
$$I = \frac{\Delta \phi}{R}$$
抵抗率を使って書き換えて
$$I = \frac{\Delta \phi S}{\rho l}$$
電気伝導度を使って書き換えます
$$\frac{I}{S} = \sigma \frac{\Delta \phi}{l}$$
左辺に電流密度、右辺に電場が出てきます。
$$i = \sigma E$$
はい。こちらが電流密度と電場の関係を表したオームの法則になります。
電流密度と電場はベクトルですので、それらの向きは一致します。(一致しない結晶もありますが、今は気にしないで行きましょう。)
実はオームの法則は電場が弱い場所でしか成り立たない法則です。
電気伝導
先ほど出た電気伝導度を導き出してみます。
金属中を動いている伝導電子に電場 \(E\) を印加します。
そうすると電荷は \(-eE\) の力を受けます。
運動方程式は
$$m\frac{dv}{dt} = -eE$$
もし、電場以外の力が働いていないとすれば
$$v = -\frac{eE}{m}t$$
となります。
電流密度 \(i = env\) に代入すると
$$i = -\frac{ne^2E}{m}t$$
になります。
しかしこれでは時間に依存してしまい、永遠に電流密度が増加してしまいます。
もちろんそんなことは現実世界ではありえません。
実際の金属中には原子が存在し、電子はその原子に衝突するからです。
何秒間に一回衝突するかはわからないので計算ができません。そこで衝突ではなく、空気抵抗のような速度に依存する力を受けていると考えてみます。
そうすると運動方程式は
$$m\frac{dv}{dt} = -eE-av$$
\(a\) は比例係数です。
摩擦力と電場による力が釣り合うと電子は等速運動します。このとき加速度はゼロですので
$$v = -\frac{e}{a}E$$
これを電流密度の式に代入すると
$$i = \frac{ne^2}{a}E$$
となります。
実はこれもオームの法則と同じ形をしていますね。
つまり \(\frac{ne^2}{a}\) が電気伝導度に対応します。
\(a\) を \(m/\tau\) とおくと
$$\sigma = \frac{ne^2\tau}{m}$$
となります。
これが電気伝導度で、 \(\tau\) は時間と同じ次元の定数でして、「タウ」と読みます。
まとめ
今回は定常電流について学びました。
そこまで難しいわけではないのでぜひマスターしましょう。









