大学受験で散々出てきたコンデンサーについて扱っていきましょう。
静電ポテンシャルから静電容量を計算していきます。
電気容量
半径 \(R\) の導体球に電荷が \(q\) があるとします。
このとき電場は
$$E = \frac{q}{4\pi \epsilon_0 R^2}$$
です。(ガウスの法則積分系を使用しました)
無限遠を基準とするとポテンシャルは
$$\phi = \frac{q}{4\pi \epsilon_0 R}$$
になります。
半径を一定とすると、電荷とポテンシャルの関係は比例関係にあるので比例定数を \(C\) とすると
$$q = C\phi$$
となります。
このとき \(C\) を電気容量といいます。
もちろん \(C\) は
$$C = 4\pi \epsilon_0 R$$
です。
静電エネルギー
次に静電エネルギーを見ていきます。
導体に電荷があるとき、その導体は静電エネルギーを持ちます。
静電エネルギーの式はこちらでした。
$$U = \frac{1}{2}q\phi$$
電気容量を使って表すと
$$U = \frac{1}{2}C\phi^2 = \frac{1}{2C}q^2$$
です。
コンデンサー
導体が2つあり、\(\pm q\) の電荷を与えます。
これら2つの導体を近づけた時、下図のように電荷が引き合い、表面に集まります。
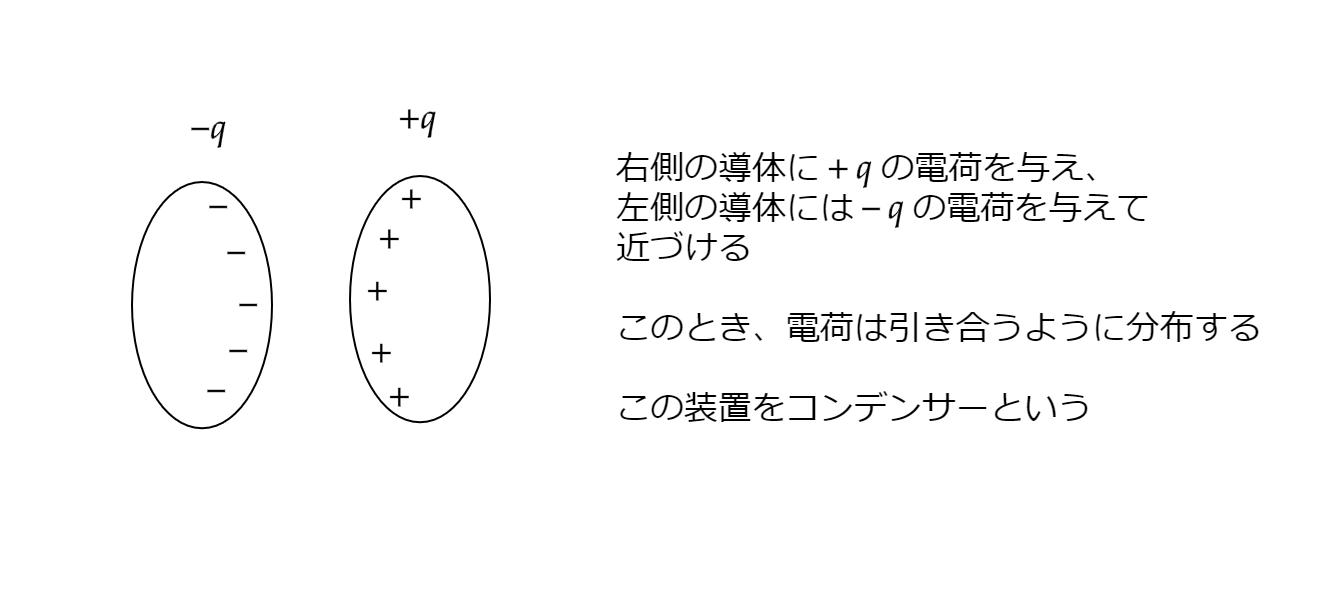
このようにして作られた装置をコンデンサーと呼び、電荷の蓄積やノイズを取り除く目的として、集積回路によく使われます。
左側の導体の電荷とポテンシャルをそれぞれ \(q_1, \phi_1\) として、右側を \(q_2, \phi_2\) とします。
そうすると電荷は
$$q_1 = C_{11}\phi_1+C_{12}\phi_2$$
$$q_2 = C_{21}\phi_1+C_{22}\phi_2$$
になります。
\(C_{12}\) は導体1の電荷が導体2のポテンシャルに比例するときの比例定数です。式で表すと
$$q_1 = C_{12}\phi_2$$
です。また、逆も成り立ちます。
$$q_2 = C_{21}\phi_1$$
いまでてきた \(C_{12}, C_{21}\) は一般的に次のような関係があります。
$$C_{12} = C_{21}$$
これを電気容量係数の相反定理と呼びます。
さてさてコンデンサーの電気容量を計算してみましょう。
まずはこの2つの式
$$q_1 = C_{11}\phi_1+C_{12}\phi_2$$
$$q_2 = C_{21}\phi_1+C_{22}\phi_2$$
からポテンシャルを左辺に持っていきます。
$$\phi_1 = \frac{q_1-C_{12}\phi_2}{C_{11}}$$
$$\phi_2 = \frac{q_2-C_{21}\phi_1}{C_{22}}$$
代入して
$$\phi_1 = \frac{q_1-C_{12}\frac{q_2-C_{21}\phi_1}{C_{22}}}{C_{11}}$$
計算します。
$$\phi_1 = \frac{q_1C_{22}-C_{12}q_2-C_{12}C_{21}\phi_1}{C_{11}C_{22}}$$
$$\phi_1(C_{11}C_{22}) = q_1C_{22}-C_{12}q_2+C_{12}C_{21}\phi_1$$
$$\phi_1(C_{11}C_{22})-C_{12}C_{21}\phi_1 = q_1C_{22}-C_{12}q_2$$
$$\phi_1 =\frac{q_1C_{22}-C_{12}q_2}{C_{11}C_{22}-C_{12}C_{21}}$$
これを \(\phi_2\) についても同様に導き出していきます。
そうすると
$$\phi_2 =\frac{q_2C_{11}-q_1C_{21}}{C_{11}C_{22}-C_{12}C_{21}}$$
となります。
相反定理より、
$$\phi_1 =\frac{q_1C_{22}-q_2C_{12}}{C_{11}C_{22}-C_{12}^2}$$
$$\phi_2 =\frac{q_2C_{11}-q_1C_{21}}{C_{11}C_{22}-C_{12}^2}$$
導体1の電荷を \(+q\), 導体2の電荷を \(-q\) とすると
$$\phi_1 =\frac{C_{22}+C_{12}}{C_{11}C_{22}-C_{12}^2}q$$
$$\phi_2 =-\frac{C_{11}+C_{21}}{C_{11}C_{22}-C_{12}^2}q$$
$$\Delta \phi = \phi_1-\phi_2 = \frac{C_{11}+C_{21}+2C_{12}}{C_{11}C_{22}-C_{12}^2}q$$
このとき、係数の逆数を \(C\) とおくと
$$C = \frac{C_{11}C_{22}-C_{12}^2}{C_{11}+C_{21}+2C_{12}}$$
つまり
$$q = C\Delta \phi$$
です。この \(C\) が電気容量です。
(少し長かったのですが計算自体は難しくなかったと思います。)
まとめ
今回はコンデンサーについて見ていきました。
入試によく出た回路の問題等はあまり見かけません。
ポテンシャル等の地道な計算をしっかりしましょう!