ここでは単振動を扱います。
単振動は非常に重要な考え方です。
確実に理解してください!!!
単振動
比例定数を \(k\) とした時の単振動の運動方程式はフックの法則より
$$m\frac{d^2x}{dt^2} = -kx$$
となります。両辺を \(m\) でわり、 \(\omega^2 = k/m\) とおけば
$$\omega = \sqrt{\frac{k}{m}}$$
$$\frac{d^2x}{dt^2} = -\omega^2x$$
となります。この式は2階の常微分方程式です。
xを2回微分するとマイナスと定数が付き、xが再び出てくるこの形は
$$x = C \sin(\omega t+\phi)$$
を代入すれば解くことができます。(cosでもOKです。)
なお、今出てきたCは実数の定数です。
この解き方は覚えてください!
常微分方程式は基本的に解法を覚えなければ解けないものが多いです。
ここからは用語の説明です。
時間の正弦関数(もしくは余弦関数)で表される運動のことを単振動といいます。
Cが振幅と呼ばれ、振動の大きさを表す定数です。
\(\omega\) を角振動数、 \(\frac{\omega}{2\pi}\) を振動数、振動数の逆数を周期といいます。
\(\omega t+\phi\) を位相、 \(\phi\) を初期位相と呼びます。
この単振動という運動は非常に重要です。
波動系の分野ではもちろん電磁気、量子力学にも出てくるので完璧に理解してほしいです。
単振り子
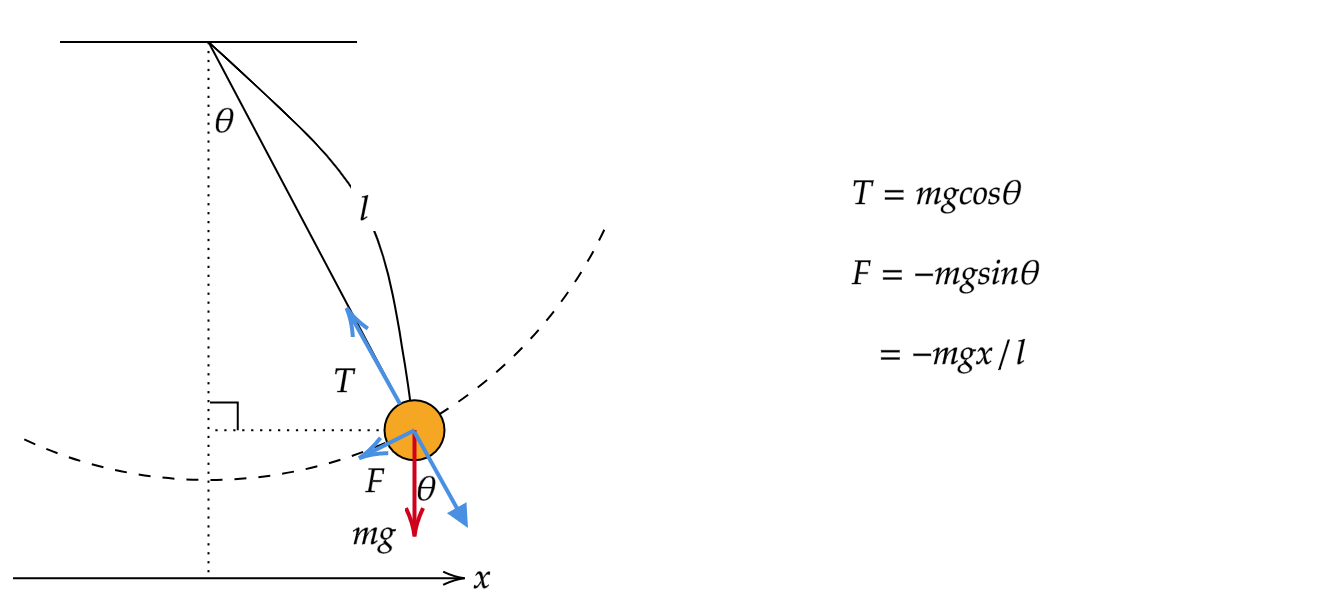
図のように小球をつるし、鉛直面内で振動させる運動を単振り子といいます。
今回は運動方程式を立て、それを解いていきたいと思います。
最下点から円弧に沿って測った長さを \(x\) とすると接線成分の運動方程式が次のようになります。
$$m\frac{d^2x}{dt^2} = -mgsin\theta$$
小球には重力が働きますよね。
それを接線成分と垂直成分(糸に平行な向き)に分けたとき、式に \(-mgsin\theta\) が出てきました。
さて \(\theta\) が小さいときの運動を考えましょう。(大きいときの運動は特別な関数が必要になるので今は取り扱いません。)
\(\theta\) が十分に小さいときに
$$\sin\theta \approx \theta$$
とみなせます。(これは非常に有名な近似ですので忘れないでください。)
そのため先ほどの式は
$$m\frac{d^2x}{dt^2} = -mg\theta$$
$$\frac{d^2(l\theta)}{dt^2} = -g\theta$$
$$\frac{d^2\theta}{dt^2} = -\frac{g}{l}\theta$$
ここで \(\frac{g}{l} = \omega^2\) と置けは単振動と一緒でsin関数を使って表せます。
$$\theta = \theta_0sin(\sqrt{\frac{g}{l}t+\phi})$$
角振動数が
$$\omega = \sqrt{\frac{g}{l}}$$
ですので振動数は
$$\nu = \frac{\omega}{2\pi} = \frac{1}{2\pi}\sqrt{\frac{g}{l}} $$
となります。最後に周期を導きます。
$$T = \frac{1}{\nu} = 2\pi \sqrt{\frac{ l}{g}}$$
はい。こちらが周期です。
これは振幅に無関係ですよね。この性質を振り子の等時性といいます。
まとめ
今回は単振動と単振り子を扱いました。
次は減衰振動と強制振動を学んでいきましょう。