今回から大学で学ぶ力学の解説をしていきます。
最初は変位と速度と加速度を扱います。
高校力学と一緒ですね。内容自体は難しくないですが、微積とベクトルの知識がなければ躓きます。
自信がない人はまず数学を勉強しましょう。
変位と速度
まずは変位から
変位とは位置ベクトルの差のことを指します。
位置ベクトルはその名の通り、位置をベクトルで表したものです。
変位を式で書くとこのようになります。
$$\Delta \mathbf{r} = \mathbf{r_1} – \mathbf{r_2}$$
ではこの変位に \(\frac{1}{\Delta t}\) をかけたものを考えてます。
\(\Delta t\) を十分短く考えた時、 \(\Delta \mathbf{r}\) は時間 \(\Delta t\) 秒間に動いた距離になります。
距離を時間で割れば速さになりますよね。
ここでの極限を考えると \(\mathbf{r}_2\) -> \(\mathbf{r}_1\) であるから
$$\mathbf{v} = \lim_{\Delta t \to 0} \frac{\Delta \mathbf{r} }{\Delta t} = \frac{d\mathbf{r}}{dt}$$
になります。
これが変位と速度の関係です。
速度の成分と位置の関係
速度と速さの違いは何でしょうか?
速度はベクトルで速さはスカラーです。
ちなみに速度を英語で \(vector\) で、速さは \(speed\) です。
このページでは基本的に速度を取り扱いますので \(\mathbf{v}\) を用います。
変位と速度の関係を見ていきましょう。
変位を i, j, k 方向に分けて考えると
$$\Delta \mathbf{r }= \Delta \mathbf{i}+ \Delta \mathbf{j} + \Delta \mathbf{k} $$
となります。極限を考えると
$$v = \lim_{\Delta t \to 0} \frac{\Delta \mathbf{r}}{\Delta t}= \frac{dx}{dt}\mathbf{i} + \frac{dx}{dt}\mathbf{j} + \frac{dx}{dt}\mathbf{k }$$
になります。
成分ごとに分けてみましょう。
$$v_x = \frac{dx}{dt}, v_y = \frac{dy}{dt}, v_z = \frac{dz}{dt} $$
となりますよね。
これで速度の成分と位置の関係を出せました。
加速度
さてさて、次は加速度を考えましょう。
速度の時間的変化を表すベクトルとして加速度が \(a\) 定義されます。
$$a = \lim_{\Delta \to t} \frac{\Delta \mathbf{v}}{\Delta t} = \frac{d\mathbf{v}}{dt}$$
ここから加速度と位置の関係を見ていきたいため、図のような質点が円上を運動する状況を考えましょう。
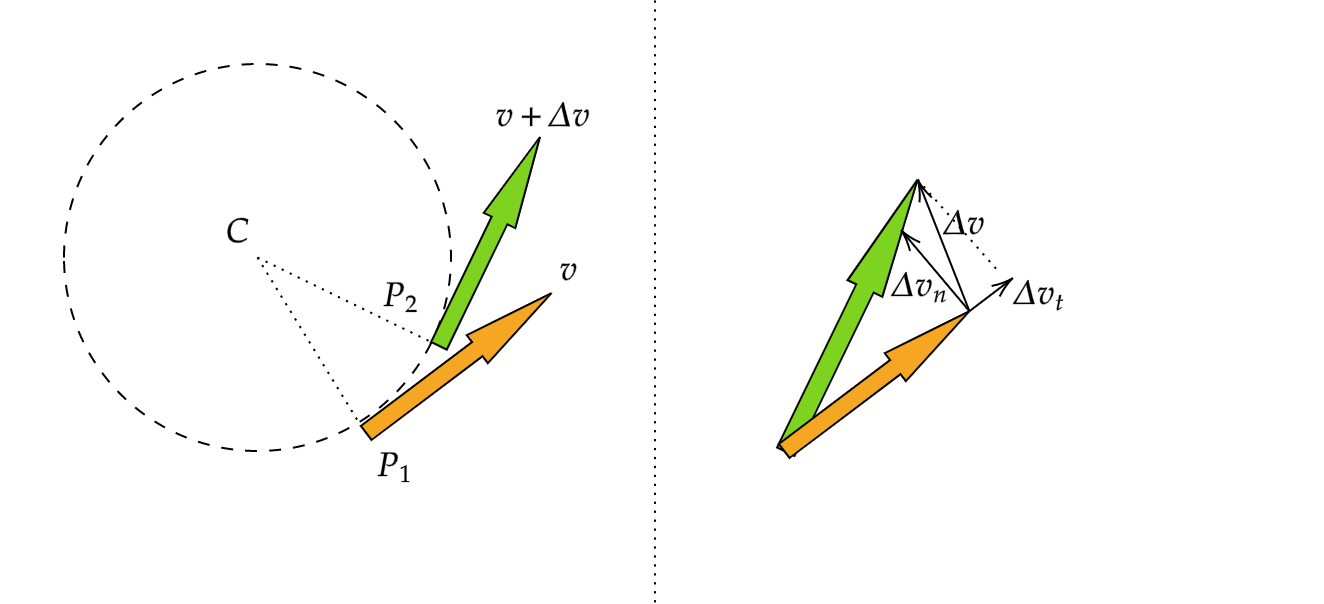
\(P_1\) を通るときその速度を \(v\) とし、 \(P_2\) を通るときの速度を \(v+\Delta v\) とする。また、それらの間の角を \(\theta\) とします。
\(\Delta v\) を \(v\) に平行な成分 \(\Delta v_t\) と垂直な \(\Delta v_n\) 成分に分けます。
\(\Delta \theta\) は十分に小さい角ですので
$$\Delta v_n = v\Delta \theta$$
とみなせます。( \(\Delta v sin \theta \approx \Delta v \theta = n_n\) となりますよ)
\(P_1\) から \(P_2\) までの長さを \(\Delta s\) とすると \(\Delta s = R\Delta \theta\)となります。
( \(R\times tan\theta = \Delta s\) より \(tan\theta\) は非常に小さいので \(\tan\theta = \tan\theta\) とみなせますよ)
急に出てきましたが \(R\) は円の半径です。
\(v_n\) と \(\Delta s\) の関係は
$$\Delta v_n = v\Delta \theta = \frac{v}{R}\Delta s$$
ですから加速度の法線成分が分かります。
$$a_n = \lim_{\Delta t \to 0}\frac{\Delta v_n}{\Delta t} = \lim_{\Delta t \to 0}\frac{v}{R}\frac{\Delta s}{\Delta t} = \frac{v^2}{R}$$
はい。これが加速度の法線成分で、高校力学にもよく出てきた関係式です。
円運動を考えるときによく出てきましたよね。
では次に接線成分を出しましょう。
$$a_t = \lim_{\Delta t \to 0}\frac{\Delta v_t}{\Delta t} = \lim_{\Delta t \to 0}\frac{v}{t} = \frac{v}{t} = \frac{d^2s}{dt^2}$$
これで位置と加速度の関係が導き出せました。
位置を時間で2回微分すれば加速度になるのですね。
まとめ
今回は位置、速度と加速度の関係を見ていきました。
時間で微分すれば出てくるので、覚え方としては簡単ですね。