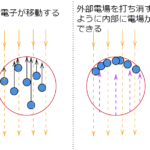
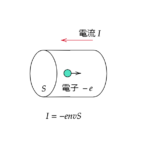
ビオサバールの法則が出てきます。
ビオ・サバールの法則
ビオ・サバールの法則は電流を流れる導線を考え、その導線の微小長さ \(\Delta s\) が作り出す磁束密度を算出することができます。
下図のように導線に電流が流れるとその周りに磁場が発生します。
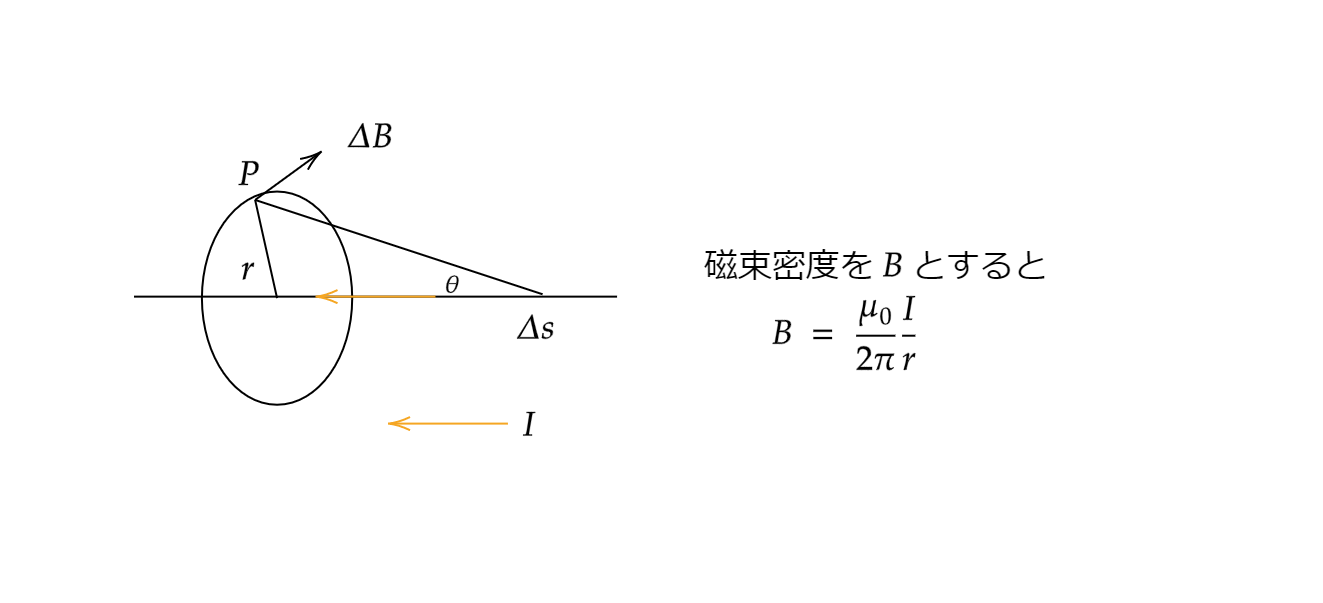
磁束密度の大きさは電流の大きさに比例し、電流からの距離に反比例します。
比例係数を \(\frac{\mu_0}{2\pi}\) とおくと磁束密度は次のように表せます。
$$B = \frac{\mu_0}{2\pi}\frac{I}{r}$$
では次に長さ \(\Delta s\) の導線に流れる電流が点Pに作り出す磁束密度を計算すると
$$\Delta B = \frac{\mu_0}{4\pi}\frac{\sin \theta}{R^2}I\Delta s$$
になります。
この磁束密度の向きは点Pの位置ベクトルを \(\vec{r}\) 、電流素片の位置ベクトルを \(\vec{r}’\) 、 電流の向きの単位ベクトルを \(\vec{t}\) とすると、磁場の向きは次のように表されます。
$$\vec{t}\times (\vec{r}-\vec{r}’)$$
\(t\) は単位ベクトルですので大きさは
$$|\vec{t}\times (\vec{r}-\vec{r}’)| = |(\vec{r}-\vec{r}’)|\sin\theta$$
です。
先ほどの式をベクトルで書けば
$$\Delta B = \frac{\mu_0}{4\pi}\frac{I\vec{t}\times (\vec{r}-\vec{r}’)}{|\vec{r}-\vec{r}’|^3}\Delta s$$
となります。
これをビオ・サバールの法則といいます。
高校電磁気学では出てこなかった法則です。慣れないて思いますのでしっかりと演習して身につけてください。
電流切片 \(\Delta s\) が作り出す磁束密度を考えましたが、ここから位置 \(\vec{r}\) に作り出す磁束密度を求めます。
といっても重ね合わせの原理より、積分すればよいだけです。
つまり次のようになります。
$$\vec{B} = \frac{\mu_0}{4\pi}\int_C \frac{I\vec{t}\times (\vec{r}-\vec{r}’)}{|\vec{r}-\vec{r}’|^3}\Delta s$$
最後にこちらを電流密度を使って表すと
$$\vec{B} = \frac{\mu_0I}{4\pi}\int_C \frac{\vec{i}\times (\vec{r}-\vec{r}’)}{|\vec{r}-\vec{r}’|^3}\Delta s$$
となります。
のちに磁場を求める式としてアンペールの法則が出てくるのですが、そちらが便利(わかりやすい)ので、ビオ・サバールの法則が忘れられがちです。
特に、微小長さ \(\Delta s\) の導線が作り出す磁場を求めたいときには使える法則ですので、是非身につけて下さい。
磁場の強さ
磁束密度 \(B\) と磁場の強さ \(H\) との関係を次のように定義します。
$$H = \frac{1}{\mu_0}B$$
これを使ってビオ・サバールの法則を表すと
$$\vec{H} = \frac{1}{4\pi}\int_C \frac{\vec{i}\times (\vec{r}-\vec{r}’)}{|\vec{r}-\vec{r}’|^3}\Delta s$$
になります。
磁場の強さ \(H\) よりも磁束密度 \(B\) の方がよく使いますが、こちらの方も覚えて下さい。
まとめ
今回はビオ・サバールの法則を学びました。
アンペールの法則と並んで磁束密度を計算するのに必要な法則ですのでぜひマスターしてください