前回はこちら!

ここでは運動量と力積について学んでいきます。
これらは高校物理でも学びましたが、改めて微分積分を交えて説明していきます。
運動量
運動量 \(p\) は次のように定義されます。
$$p = m\frac{dr}{dt} =mv$$
運動エネルギー \(\frac{1}{2}mv^2\) と間違えやすいので気を付けてください。
運動量はベクトルです。
つまり大きさと向きを持ちます。
しかし、エネルギーは速度を2乗しているのでスカラーになります。
また、2つの物体がぶつかった時にはエネルギーが熱や音に代わるため、運動エネルギーは保存されません。
この運動量を運動方程式に取り入れてみると、このようになります。
$$\frac{dp}{dt} = F$$
よりシンプルになりましたね。
運動量はベクトルですので2つの物体の衝突や分離など、向きに関する現象を取り扱うときによく出てきます。
力積
微小時間の間に受けた力を力積といいます。
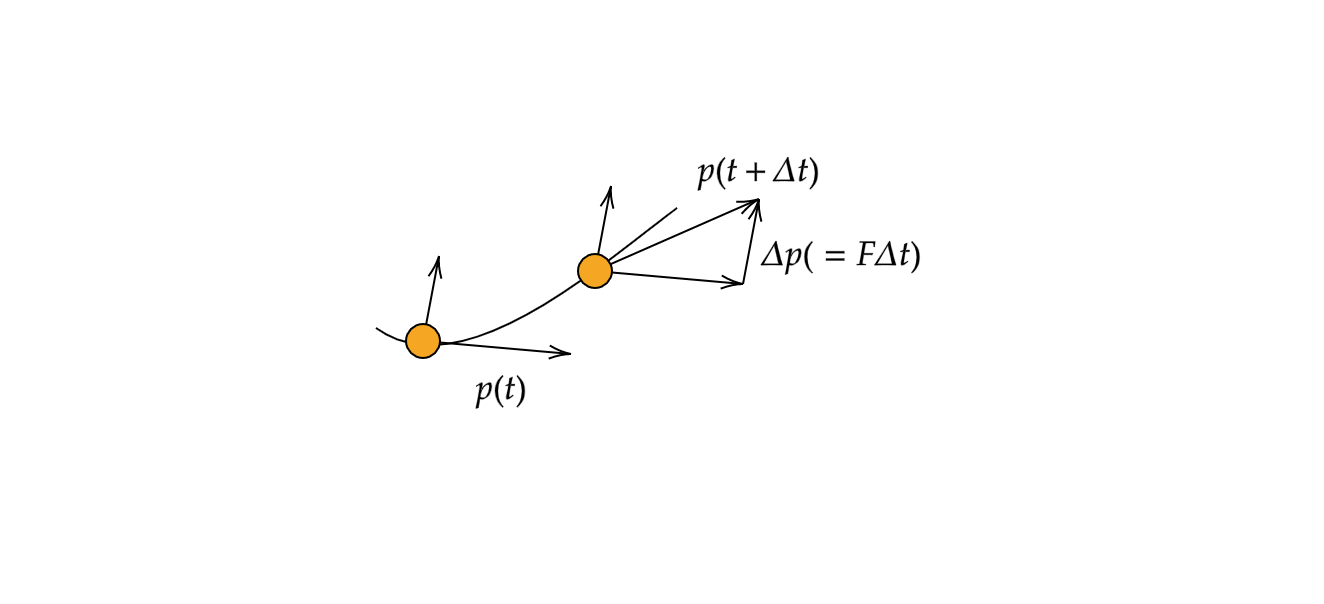
式で表します。
$$\frac{dp}{dt} = \lim_{\Delta t -> 0}\frac{\Delta p}{\Delta t} \approx \frac{\Delta p}{\Delta t}$$
ただし、
$$\Delta p = p(t + \Delta t)-p(t)$$
です。
これらから力積が分かります。
$$\Delta p \approx F\Delta t$$
上記の式の右辺が力積です。
では力積を積分形式で書いてみましょう。
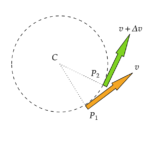
時間 \(t_1\) のときの運動量を \(p_1\) とし、時間 \(t_2\) の時の運動量を \(p_2\) とすると力積を次のように表せます。
$$p_2-p_1 = \int^{t_2}_{t_1} F(t)dt$$
そこまで難しくないですね。
ちなみに野球のボールをバットで打つように、短い時間のみ働く力を撃力といいます。
摩擦がある運動
摩擦
最後に摩擦がある運動を考えていきましょう。
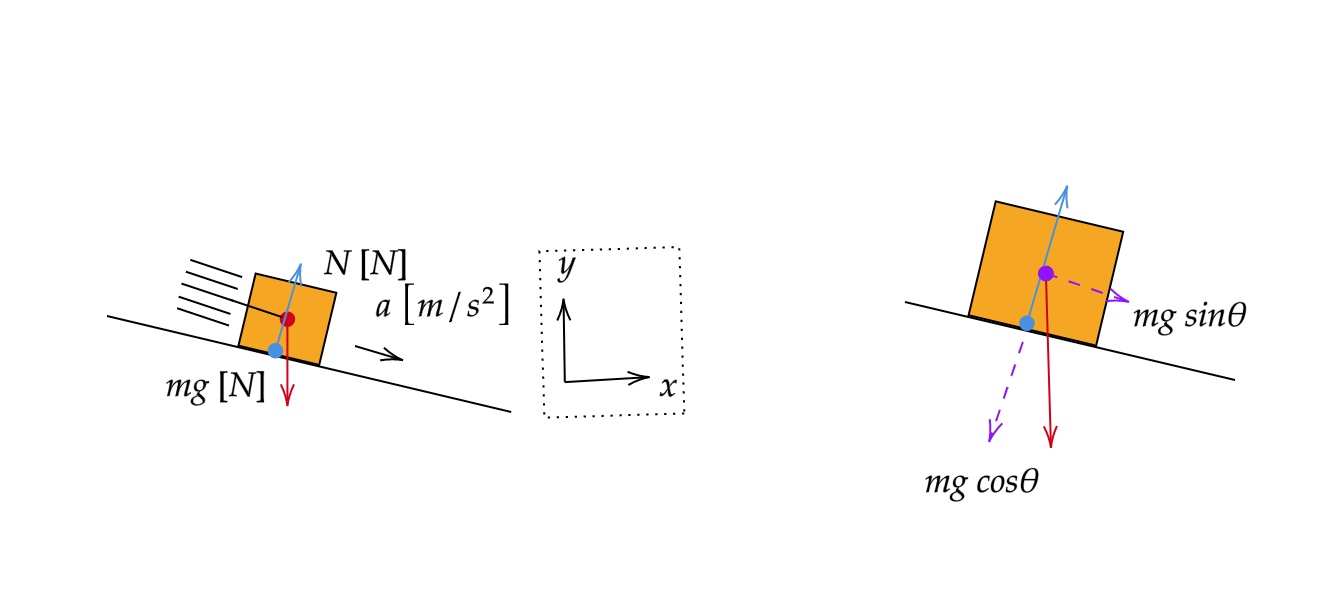
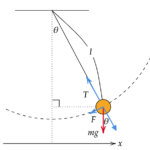
図のように摩擦がある粗い斜面を滑る物体の運動を考えましょう。
この時に働く力は3つあります。
1つ目は重力。これは大丈夫ですね。
2つ目は垂直抗力。名前の通り斜面に垂直な方向に働く力です。よって
3つ目は摩擦力。粗い斜面といったら摩擦がある場合が多いです。
これらの力の大きさを考えていきましょう。
まず重力の大きさは分かりますよね。
質量×重力加速度で表せます。
次に着目すべき点は垂直抗力と摩擦力のなす角です。
その角は90度ですので垂直抗力と摩擦力のつり合いの式は別々でたてられます。
よって斜面に垂直な成分のつり合いの式は垂直抗力を \(N\) とすると
$$mg\cos\theta = N$$
となります。
一方斜面に水平な成分の運動方程式は次のようになります。
$$m\frac{d^2x}{dt^2} = mg\sin\theta ~-~ \mu mg\cos\theta$$
右辺第2項にでてきた \(\mu\) は動摩擦係数と呼ばれます。
実は摩擦の大きさは摩擦力係数×垂直抗力で算出できます。
積分して速度を出してみましょう
$$\int m\frac{d^2x}{dt^2} dt= \int mg\sin\theta ~-~ \mu mg\cos\theta dt$$
$$\frac{dx}{dt} = (g\sin\theta ~-~ \mu mg\cos\theta ) t$$
さらに積分をして距離を出しましょう。
$$\int \frac{dx}{dt} dt= \int (g\sin\theta ~-~ \mu mg\cos\theta ) t dt$$
$$x = \frac{1}{2} (g\sin\theta ~-~ \mu mg\cos\theta ) t^2 $$
まとめ
今回は運動量と力積について見ていきました。
次は大事な単振動を学びます!
次回はこちら![大学力学]1-4. 単振動