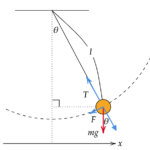
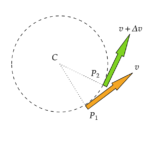
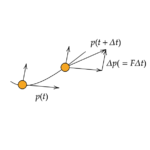
今回は運動の法則について学びます。
まずはニュートンの運動の3法則を見ていきましょう。
運動の3法則
第1法則
第1法則は慣性の法則ともいわれています。
その内容を日本語で書くと
外部からの影響を受けていない物体は静止または等速運動を続ける
というものです。
第2法則
第2法則は運動方程式に関する法則です。
物体が力を受けるとその力の向きに加速度が生じる
また、その大きさは力の大きさに比例し、質量に反比例する
といったものです。式で表すと
$$ma=F$$
これは超有名ですね。
単位には気を付けましょう。
質量が[kg]、加速度は[m/s^2]、力は[N](ニュートン)です。
第3法則
第3法則は作用反作用の法則です。
作用(加えた力)に対して大きさが同じで向きが真逆のベクトルを反作用といいます。
放物運動
運動の3法則だけではページが余ってしまうので、放物運動も一緒に勉強しましょう。
高校物理では自由落下や水平投射を考えましたが斜方投射さえ分かれば他が全部わかるので、斜方投射を扱います。
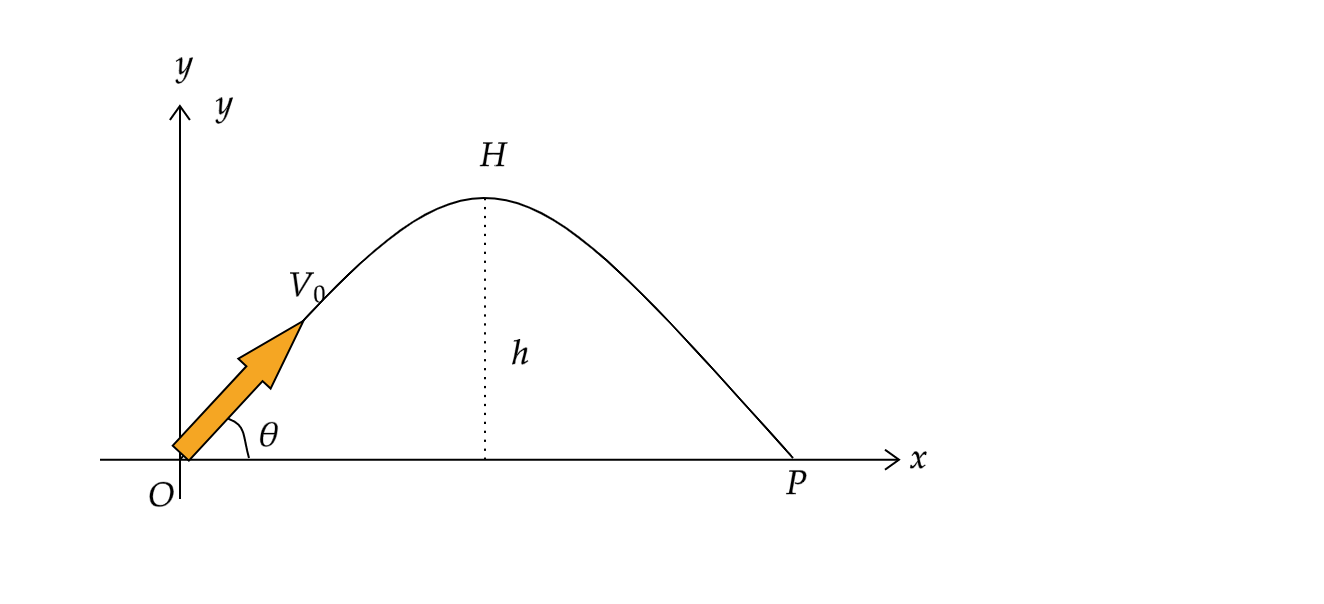
初速度で \(V_0\) 小球を投げた時の軌跡を図に書きました。
最大の高さは \(h\) で、初期位置は原点とします。
なお、\(t = 0\) のときに与えられる条件を初期条件といいます。
速度の初期条件を初速度といいます。
(初期条件はこの先たくさん出てくる言葉ですので絶対に忘れないでください!)
この図における初期条件は
$$x=0, ~~~y=0$$
$$v_x = V_0 cos\theta, ~~~v_y = V_0sin\theta$$
となります。
重力は常に鉛直下向きに働きます。
しかし、y軸は上向きを正としましたので、力は次のようになります。
$$F_x = 0, ~~~F_y = -mg$$
\(F_x\) は外部から力を加えていないのではもちろんゼロですよね。
一方、\(F_y\) はどうでしょうか。
y軸方向には重力が働くので運動方程式より下向きにの力が働きます。
なお、は重力加速度と呼ばれ、その値は約9.8m/s^2です。
場所によって違ったりしますがこれは後程学びます。(コリオリの力らへんで学びます。)
積分をして放物運動を考える
加速度を微分系で書くことにしましょう。
そうすると
$$a_x = \frac{d^2x}{dt^2} = 0,~~~a_y = \frac{d^2y}{dt^2} = -g$$
となります。
ここから時間について積分していきます。
$$\int \frac{d^2x}{dt^2} dt = 0\\ \frac{dx}{dt} = C_1 $$
また、
$$v_x = \frac{dx}{dt}$$
ですので結果は
$$v_x = C_1$$
が導かれます。y軸方向も同様に計算すると
$$v_y = -gt + C_2$$
となります。
先ほど出てきた初期条件を当てはめると
$$C_1 = V_0cos\theta, ~~~C_2 = V_0sin\theta$$
となります。
さてさて、もう一度積分して位置を出してみましょう。
$$\int \frac{dx}{dt} dt = \int V_0cos\theta dt = V_0t cos\theta + C_3$$
y軸方向も考えましょう
$$\int \frac{dy}{dt} dt = \int (V_0sin\theta -gt)dt = V_0t sin\theta -\frac{1}{2}gt^2+ C_4$$
またまた初期条件から積分定数を消しましょう。
初期条件では原点から投げているので初期位置は 0 です。
そのためはゼロになります。
結局以下のようになります。
$$x = V_0t~cos\theta, ~~~y = V_0t~sin\theta – \frac{1}{2}gt^2$$
これで放物線の式が出ましたが最高点に達する時間と最高点の高さを算出してみましょう。
最高点の特徴は何かを考えれば時間が導けます。
最高点ではがゼロになります。そのため式のにゼロを代入しましょう。
$$t_max = \frac{V_0}{g}sin\theta$$
これを使えば最高点の高さが得られます。
$$h = \frac{V_0^2}{2g}sin^2\theta$$
まとめ
今回は運動の3法則と放物運動について学びました。
計算自体は難しくないので確実にできるようにしてください