ここでは導体を取り扱います。
導体とは電気を通すことができる物体のことです。
導体の性質
改めて書きますと、導体とは電気を通すことができる物体のことです。
分かりやすい例は金属です。
銅や銀、金などは伝導率が高いことで有名です。
そんな導体には様々な性質があるのでそれらを見ていきましょう。
一様な電場中に導体を置くと次のようなことが分かります。
・導体内部の電場がゼロ
・導体内部ではポテンシャルが一定
・導体の表面もポテンシャルが一定
一つずつ見ていきます。
導体内部の電場がゼロ
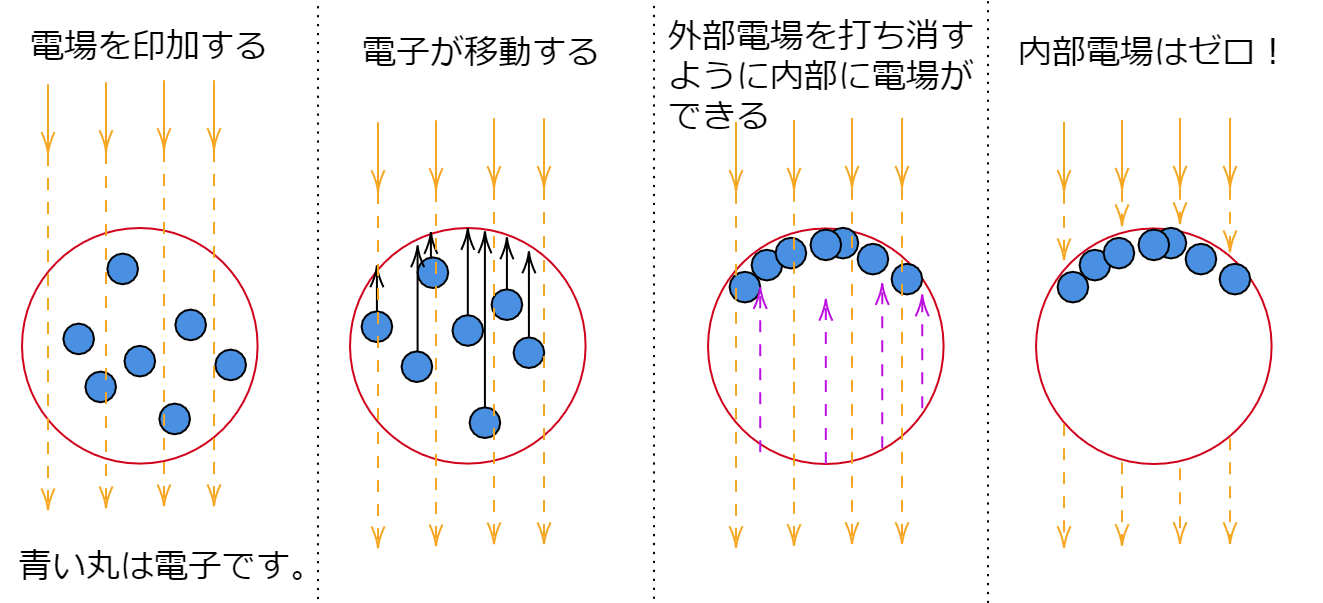
導体の内部に伝導電子がある場合を考えます。
外部電場から力を受けて、内部にある伝導電子は導体の表面に移動します。
すると内部の電子による電場が作られ、その電場と外部の電場が打ち消しあいます。
そのため内部の電場はゼロになります。
$$E_{int} + E_{ext} = E_{sum} = 0$$
図で確認しましょう。
導体のポテンシャルが一定
電場を積分するとポテンシャルになりますよね。
内部の電場がゼロであるということは、ポテンシャルが一定になります。
導体表面の電場
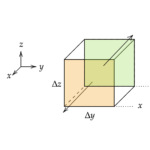
電荷が導体の表面に面密度 \(\sigma\) で分布しているとしましょう。
このとき、ガウスの法則を適用して、導体表面の電場を考えます。
ガウスの法則の積分系より
$$\int_S(\vec{E}\cdot \vec{n})dS = \frac{1}{\epsilon_0}\sigma \Delta S$$
よって
$$E\Delta S = \frac{1}{\epsilon_0}\sigma \Delta S$$
電場の強さが分かります。
$$E = \frac{\sigma}{\epsilon_0}$$
このように表面での電場の強さは一定です。
境界値問題・鏡像法
導体の電場を求めるとき、導体の内部と外部の境界に注目して問題を解くことを境界値問題などと呼びます。
この境界値という言葉はもっと一般的で、何かの境界に注目して問題を解くことが物理ではよくあります。
境界値問題を一問解いてみましょう。
図のように無限に広がっている導体の表面から距離 y’ の位置に点電荷 \(q\) が置かれているときに生じる電場と導体表面の電荷密度を求めましょう。
解き方
導体がないものとして、距離 -y’ の位置に点電荷 \(-q\) を置いたとします。
このとき、y>0 の空間におけるポテンシャルは
$$\phi(x,y,z) = \frac{q}{4\pi \epsilon_0}{\frac{1}{\sqrt{x^2+(y-y’)^2+z^2}-\frac{1}{\sqrt{x^2+(y+y’)^2+z^2}}$$
となります。
y成分の電場は
$$E_y(x,y,z) = -\frac{\partial \phi(x,y,z)}{\partial y} = \frac{q}{4\pi \epsilon_0}{\frac{y-y’}{{x^2+(y-y’)^2+z^2}^{\frac{3}{2}}-\frac{1}{x^2+(y+y’)^2+z^2}^{\frac{3}{2}}$$
とくに導体表面では
$$E_y(x,0,z) = -\frac{\partial \phi(x,y,z)}{\partial y} = \frac{q}{2\pi \epsilon_0}{\frac{y’}{{x^2+(y’)^2+z^2}^{\frac{3}{2}}$$
です。電荷密度は
$$\sigma(x,y) = \epsilon_0 E_y(x,0,z) = \frac{q}{2\pi}{\frac{y’}{{x^2+(y’)^2+z^2}^{\frac{3}{2}}$$
となります。
このように導体面を鏡のように見立て、反対側の位置に同じ大きさの電荷を置いて、問題を解く方法を鏡像法といいます。
まとめ
今回は導体を取り扱いました。
導体の性質をよく理解しましょう。