ここからガウスの法則の微分系が出てきます。
最初に学習したのは積分系でした。
微分系は形こそ変わりますが、電荷と電場の関係式であることには変わりません。
ガウスの微分系の導出
電荷が空間に連続的に分布しているときのガウスの積分系の法則は
$$\int_S\vec{E}\cdot \vec{n} dS = \frac{1}{\epsilon_0}\int_V \rho dV$$
でした。
ここからガウスの法則(微分系)を導き出しましょう。
体積が \(\Delta V = \Delta x+\Delta y+\Delta z\) の微小な物体があるとします。
面積が \(\Delta y\times \Delta z\) で与えられる長方形 \(S_x\) を貫く電場の強さを考えます。
下図のように軸を取ると、長方形 \(S_x\) を通る電場は図のように \(E_x(x+\Delta x)\Delta y \Delta z – E_x(x)\Delta y \Delta z)\) で表せます。
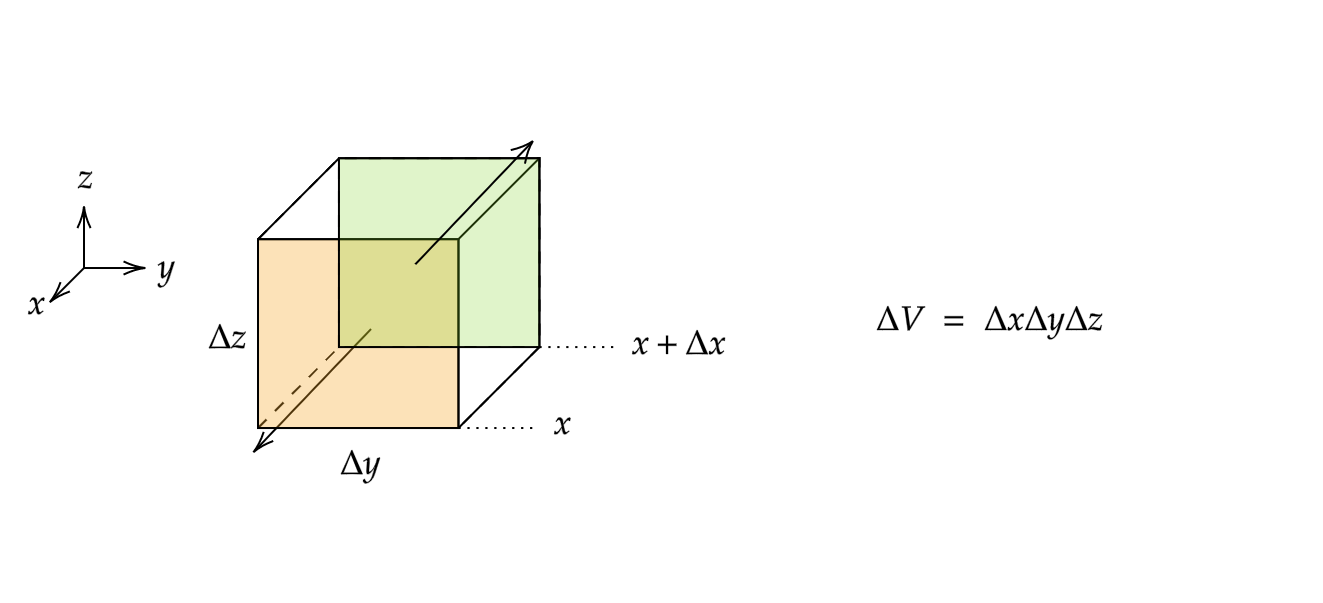
これを式変形させます。
$$\begin{align}E_x(x+\Delta x)\Delta y \Delta z-E_x(x)\Delta y \Delta z &= (E_x(x+\Delta x)-E_x(x))\Delta y \Delta z \\\\ &= \frac{E_x(x+\Delta x)-E_x(x)}{\Delta x}\Delta x \Delta y \Delta z \\ &= [\frac{\partial E_x}{\partial x}]_0\Delta V \end{align}$$
最後は次の近似を使います。
$$E_x(x+\Delta x) \approx E_x(x)+[\frac{dE_x(x)}{dx}]_0\Delta x$$
この近似を使うと
$$\begin{align}\frac{E_x(x+\Delta x)-E_x(x)}{\Delta x} &= \frac{E_x(x)+[\frac{dE_x(x)}{dx}]_0\Delta x-E_x(x)}{\Delta x}\\ &= \frac{[\frac{dE_x(x)}{dx}]_0\Delta x}{\Delta x} \\\\ &= [\frac{\partial E_x(x)}{\partial x}]_0\end{align}$$
いま x 軸について考えましたので、y, z も同様に計算してみます。
そうすると微小体積 \(\Delta V\) を貫く電場の強さは
$$[\frac{\partial E_x(x)}{\partial x}]_0+[\frac{\partial E_y(y)}{\partial y}]_0+[\frac{\partial E_z(z)}{\partial z}]_0$$
になります。
これをナブラ演算子を使って書くと以下のようになります。
$$\nabla\cdot \vec{E}(r) = [\frac{\partial E_x(r)}{\partial x}]_0+[\frac{\partial E_y(r)}{\partial y}]_0+[\frac{\partial E_z(r)}{\partial z}]_0$$
したがってガウスの積分系の左辺は
$$\int_S\vec{E}\cdot \vec{n} dS = \nabla \cdot \vec{E} \Delta V$$
になります。
右辺は
$$\frac{1}{\epsilon_0}\rho \Delta V$$
です。
よってガウスの微分の法則は次のようになります。
$$\nabla \cdot E = \frac{1}{\epsilon_0}\rho$$
以上で導けました。これは電荷があれば、その周りに電場ができることを意味する式です。
電束密度 \(D\) というものを次のように定義します。
$$D = E\epsilon_0$$
を使って表すと次のようになります。
$$\nabla \cdot D = \rho$$
凄くシンプルですね。この形でもよく出てきますので覚えておいてください。
渦なしの法則
任意の閉じた経路について渦なしの法則が成り立ちます。
$$\int_C \vec{E}\cdot \vec{t} ds =0$$
これにストークスの定理を使うと次のようになります。
$$\int_S(\nabla \times \vec{E})\cdot \vec{n} dS = 0$$
これが成り立つには()の中がゼロである必要があります。
よって、
$$\nabla \times \vec{E} = 0$$
となります。
ナブラ演算子と電場ベクトルの間に掛け算の × マークみたいなものがありますよね。
これはこれは外積の記号です。ナブラ演算子と一緒に使われる場合は回転と呼ばれます。
実はこの渦なしの法則は電磁気学の中で重要な4つの方程式のうちのひとつです。
(ストークスの定理とは線積分と面積分をつなぐ関係式で、電場に対して使うと
$$\int_S(\nabla \times \vec{E})\cdot \vec{n} dS = \int_C \vec{E}\cdot \vec{t}ds$$
となります。)
ポアソンの方程式・ラプラスの方程式
静電ポテンシャルを微分すれば電場になりますよね。
$$E = -\nabla \phi$$
これを微分系のガウスの法則に入れてみます。
$$\nabla\cdot (-\nabla \phi) = \frac{1}{\epsilon_0}\rho$$
左辺を展開していきます。
$$\begin{align}\nabla\cdot (-\nabla \phi) &= \frac{\partial}{\partial x}(-\frac{\partial \phi}{\partial x})+\frac{\partial}{\partial y}(-\frac{\partial \phi}{\partial y})+\frac{\partial}{\partial z}(-\frac{\partial \phi}{\partial z}) \\ &= -(\frac{\partial^2 \phi}{\partial x^2}+\frac{\partial^2 \phi}{\partial y^2}+\frac{\partial^2 \phi}{\partial z^2}) \\ &= -\nabla^2 \phi \end{align}$$
したがって次のようになります。
$$\nabla^2 \phi = -\frac{1}{\epsilon_0}\rho$$
これをポアソンの方程式と呼びます。
もう一つ名前が付いた方程式があるので覚えましょう。
電荷がない場合はラプラスの方程式と呼ばれます。
右辺を落とせばよいので、ラプラスの方程式は
$$\nabla^2 \phi = 0$$
です。
まとめ
今回はガウスの微分法則からラプラスの方程式までを勉強しました。
式を覚えるだけでなく、導出できるようにしてください!








