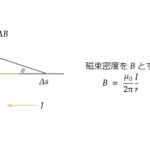
今回は自己インダクタンス、相互インダクタンスについて説明していきます。
自己インダクタンス
閉じた回路に電流を流した時、周りに磁場が生じます。
その磁場は自分自身の閉じた回路を貫き
$$\Phi = LI$$
と表されます。
このとき \(L\) を自己インダクタンスと呼びます。
電流が時間変化すると、磁束も同様に時間変化するので起電力が生じるます。これは次のように表されます。
$$\phi_e = -\frac{d\Phi}{dt} = -L\frac{dI}{dt}$$
マイナスが付いているということは起電力は電流が増える向きとは逆向きに生じます。
この現象を自己誘導といいます。
相互インダクタンス
自分自身の閉回路に起電力が生じるのであれば、その隣に同じく閉回路2を置けばそこにも電流が流れるでしょう。
回路2の磁束を \(\Phi_2\) とすると
$$\Phi_2 = L_{21}I_1$$
と表されます。
\(L_{21}\) を相互インダクタンスと呼びます。
逆に閉回路2に電流を流せば閉回路1にも起電力が生じます。
$$\Phi_1 = L_{12}I_2$$
と表されます。
このときでてきた \(L_{12}\) も相互インダクタンスと呼ばれます。
磁束が時間変化すると起電力が生じるので閉回路2の誘導起電力は次のように表されます。
$$\phi_{e2} = -\frac{d\Phi_{2}}{dt} = -L_{21}\frac{dI_{1}}{dt}$$
これもまた、マイナスが付いているので起電力は電流が増える向きとは逆向きに生じます。
このように一つの回路から生じる電流が別の回路の起電力を作り出す現象を相互誘導といいます。
相互インダクタンスが \(L_{12}\) と \(L_{21}\) の2つが出てきますが、実はどちらも同じです。
一般的には相互インダクタンスを \(M\) で表します。
$$L_{12} = L_{21} = M$$
これが成り立つ証明をこれからしてみましょう。
相反定理の証明
今出てきた相互インダクタンスの相反定理の証明をします。
回路1について、ベクトルポテンシャルを使うと
$$\vec{B} = \nabla \times \vec{A}$$
$$\vec{A} = \frac{\mu_0 I_1}{4\pi}\int \frac{\vec{t_1}}{|\vec{r}-\vec{r’}|}ds’$$
回路2を貫く磁束は
$$\begin{align}\Phi_2 &= \int \vec{B}\cdot \vec{n_2} dS\\ &=\int \nabla \times \vec{A}\cdot dS \\&= \int \vec{A}\cdot\vec{t_2}ds \\&=\frac{\mu_0 I_1}{4\pi}\int \int \frac{\vec{t_1}\cdot \vec{t_2}}{|\vec{r}-\vec{r’}|}ds’ds \end{align}$$
よって、相互インダクタンスは
$$L_{21} = \frac{\mu_0}{4\pi}\int \int \frac{\vec{t_1}\cdot \vec{t_2}}{|\vec{r}-\vec{r’}|}ds’ds $$
です。回路2に電流を流した場合も同様に計算すると同じ結果が得られます。
これより、相反定理が成り立つことが分かります。
途中でストークスの定理を使いました。
まとめ
今回はインダクタンスを学びました。
相反定理の計算はやや面倒くさいですが、できるようにしましょう!