磁気双極子を学びます。
磁気双極子
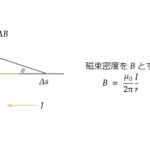
ABに流れる電流素子の位置ベクトル \(r’\) は
ABに流れている電流素子が点 \(r\) 作り出す磁場は次のように表せます。
$$\frac{\mu_0Ia}{4\pi}\frac{\vec{e_y}\times \vec{r}-(a/2)\vec{e_x}}{|\vec{r}-(a/2)\vec{e_x}|^3}$$
このままでは分母の計算ができないので、工夫をします。
途中で近似計算が出てきます。
$$\begin{align}|\vec{r}-(a/2)e_x|^2 &= {(|\vec{r}-(a/2)e_x|^2)}^{-\frac{3}{2}} \\ &= {((\vec{r}-(a/2)e_x)\cdot (\vec{r}-(a/2)e_x))}^{-\frac{3}{2}} \\ &\approx {(r^2-a(\vec{r}\cdot \vec{e_x})}^{-\frac{3}{2}} \\ &= \frac{1}{r^3}{(1-\frac{a(\vec{r}\cdot \vec{e_x})}{r^2})}^{-\frac{3}{2}} \\ &\approx \frac{1}{r^3}(1-\frac{3a(\vec{r}\cdot \vec{e_x})}{2r^2}) \end{align}$$
はい。ややめんどくさいですが計算し終わりました。
これをBC, CD, DAに流れる電流素子作り出す磁場の大きさも同様に求められます。
全部を足し合わせると
$$\vec{e_y}\times (\vec{r}-\frac{a}{2}e_x)(1+\frac{3a}{2}\frac{\vec{r}\cdot \vec{e_x}}{r^2})-\vec{e_x}\times (\vec{r}-\frac{a}{2}e_y)(1+\frac{3a}{2}\frac{\vec{r}\cdot \vec{e_y}}{r^2}) \\ -\vec{e_y}\times (\vec{r}-\frac{a}{2}e_x)(1+\frac{3a}{2}\frac{\vec{r}\cdot \vec{e_x}}{r^2})+\vec{e_x}\times (\vec{r}-\frac{a}{2}e_y)(1+\frac{3a}{2}\frac{\vec{r}\cdot \vec{e_y}}{r^2})$$
$$\approx 2a(e_x\times e_y)+\frac{3a}{r^2}(\vec{r}\cdot \vec{e_x})\vec{e_y}-(\vec{r}\cdot \vec{e_y})\vec{e_x}\times \vec{r}$$
ここでベクトル三重積の公式を思い出してください。確かこんなやつでした。
$$(\vec{a}\times \vec{b})\times \vec{c} = (\vec{a}\cdot \vec{c})\vec{b}-(\vec{b}\cdot \vec{c})\vec{a}$$
これを使うと
$$\approx 2a(e_x\times e_y)+\frac{3a}{r^2}((\vec{e_x}\times \vec{e_y})\times \vec{r})\times \vec{r}$$
()の中身を計算すると
$$=2a(e_x\times e_y)+\frac{3a}{r^2}((\vec{e_x}\cdot \vec{e_y})\vec{r})-\vec{n}r^2$$
$$=-a\vec{n}+\frac{3a}{r^2}(\vec{n}\cdot \vec{r})\vec{r}$$
したがって
$$B=-\frac{\mu_0Ia^2}{4\pi r^2}(\vec{n}+\frac{3a}{r^2}(\vec{n}\cdot \vec{r})\vec{r})$$
となります。
長かったですがこれで区切りが付きました。
偶力のモーメント
磁場中に置いた小さな回転電流(導線を円にしてそこに電流を流す)に働く偶力のモーメントは
$$N = IS\vec{n}\times\vec{B}$$
です。
ここでベクトル \(m\) を次のように定義します。
$$m = \mu_0ISn$$
そうすると磁場は
$$B=-\frac{1}{4\pi r^2}(\vec{m}+\frac{3a}{r^2}(\vec{m}\cdot \vec{r})\vec{r})$$
これを磁場の強さ \(H\) によって書き換えると
$$N=m\times H$$
となります。ここででてきた \(m\) は電場における電気双極子と同じ形をしています。
なので \(m\) を磁気双極子と呼びます。
まとめ
今回は磁気双極子について学びました。