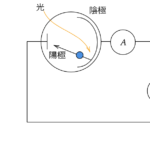
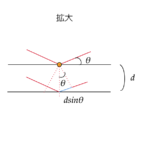
今回は原子の構造を見ていきます。
前回はこちら!5-2.X線~粒子性と波動性の二重性
用語集
| 用語 | 説明 | 用語 | 説明 | |
| 線スペクトル | 輝いている線がとびとびに現れること | リュードベリ定数 | スペクトル系列を表す公式の中に現れる定数。リュードベリはスウェーデンの物理学者 | |
| ボーアの量子条件 | 電子軌道の円周の長さが波長の整数倍に一致したとき、原子核が安定すること | 定常状態 | ボーアの量子条件に一致した状態 | |
| エネルギー準位 | 定常状態の時の電子のエネルギー | ボーアの振動条件 | 定常状態のエネルギーがそれよりも低い定常状態に移るとき、エネルギーを放出するというもの | |
| 基底状態 | 量子数が1のときの定常状態のこと | 励起状態 | 量子数が2以上のときの定常状態のこと |
しっかり覚えましょう!
水素原子のスペクトル
水素原子は原子の中で最も簡単な構造をしています。
スイスの物理学者バルマーは水素の可視光線の領域の線スペクトル(輝いている線がとびとびに現われること)を調べ、その波長には次のような規則性があることが分かりました。
$$\lambda = 3.65\times 10^{-7}\times \frac{n^2}{n^2-2^2}$$
(n =3, 4, 5…)です。
このスペクトルはバルマー系列と呼ばれます。
その後ライマンとパッシェンによって可視光線以外の領域においても水素原子のスペクトルが見つかりました。
これらより一般化すると次の式が導けます
$$\frac{1}{\lambda} = R(\frac{1}{n’^2}-\frac{1}{n^2})$$
ここで出てきた R はリュードベリ定数と呼ばれています。
n’ = 1のときをライマン系列、n’ = 2のときをバルマー系列、n’ = 3のときをパッシェン系列といいます。
ボーアの原子模型
次に原子の模型を決めるためにデンマークの物理学者ボーアが考えた仮説を見ていきます。
電子が原子核の周りを円運動すると電磁波が放射してエネルギーを失うことが知られています。
ボーアは次の仮説をもとに原子模型を提唱しました。
仮説の内容
電子は原子核を中心に等速円運動しており、質量を m, 速さを v, プランク定数を h とし、 nを正の整数とするとき次の条件を満たしています。
$$mvr = n\frac{h}{2\pi}$$
これをボーアの量子条件といい、nを量子数といいます。
また、これを満たす電子の状態を定常状態と呼びます。
この状態にある電子は安定しているので外に電磁波を放出しません。
この式を説明をするために少し式変形します。
右辺の分母を左辺と交換すると次のようになります。
$$2\pi r = n\frac{h}{mv}$$
\(\frac{h}{mv}\) が波長に当たり、量子数 n は整数を取ります。
このとき左辺は \(2\pi r\) ですので原子核の円周を表しています。
つまりボーアの量子条件は、電子の軌道の円周の長さが波長の整数倍になるとき、安定した定常状態になるという意味の式です。
また、定常状態の時の電子のエネルギーをエネルギー準位といいます。
ボーアの仮説②
2つ目はエネルギー準位に関する仮説です。
エネルギー \(E\) の定常状態から、それよりも低い \(E’\) の定常状態に移るときにその差に等しいエネルギー \(h\nu\) を放出する。
$$E-E’ = h\nu$$
というものです。
これをボーアの振動数条件といいます。
また、エネルギーが高い状態に移るときは放出ではなく吸収が起こります。
シンプルで覚えやすいですね。
最後にもう2つほど覚えてほしい用語があります。
ひとつが基底状態です。
n = 1のとき、つまり最もエネルギー準位が低いときを基底状態と呼びます。
逆に基底状態ではないとき、量子数 n が2以上のときを励起状態といいます。
正直入試にはほとんど出てきませんが、大学で習う量子力学では重要用語ですので、頭の片隅にでも入れておいてください。
まとめ
今回は水素原子のスペクトルとボーアの原子模型について学びました。
原子分野はもう折り返し地点まで来ています。
もう少しで高校物理の内容が終了するので頑張ってください。
次回はこちら!5-4.原子核と放射線