前回はこちら!1-10万有引力
ここから熱力学に入ります。
教科書によっては力学の最後に取り入れているのですが当サイトでは力学と熱力学を分けています。
用語集
物理というより化学っぽい分野です。
しっかりと覚えましょう!
| 用語・公式 | 説明 |
| 熱運動 | 原子や分子が行う無秩序な運動のこと |
| 絶対温度 | 全ての物質が凍る温度をゼロとした時の温度\((T=t+273.15)\) |
| 熱平衡 | 高温の物体と低温の物体を接触させ放置した時、2つの物体の温度が等しくなることを熱平衡の状態にあるという |
| 熱 | 物体の間で移動する熱運動のエネルギー。ちなみにその量を熱量という |
| 線膨張・体膨張 | 熱を加えると物体が膨張すること \(l=l_0(1+\alpha t) , V=V_0(1+\beta t)\) |
| 線膨張率・体膨張率 | 上の式で出てきた \(\alpha ,\beta \) のこと。物質によって決まっている |
熱と温度
絶対温度
みなさんがいつも使っている温度をセルシウス温度と呼び、単位は[℃]で表します。
しかし、物理では絶対温度 \(T\) [K]をよく使います。
すべての物質が凍る温度をゼロとしたときの温度で、普段使っている温度とこのような関係があります。
$$T=t+273.15\tag{1}$$
絶対温度=セルシウス温度+273.15です。ただし問題の多くは273.15ではなくて273を使います。
これから温度は絶対温度を使いましょう!
線・体膨張
温度が上がると物質内の粒子の運動が激しくなり、物体の長さや体積が膨張します。
これを熱膨張と呼びます。
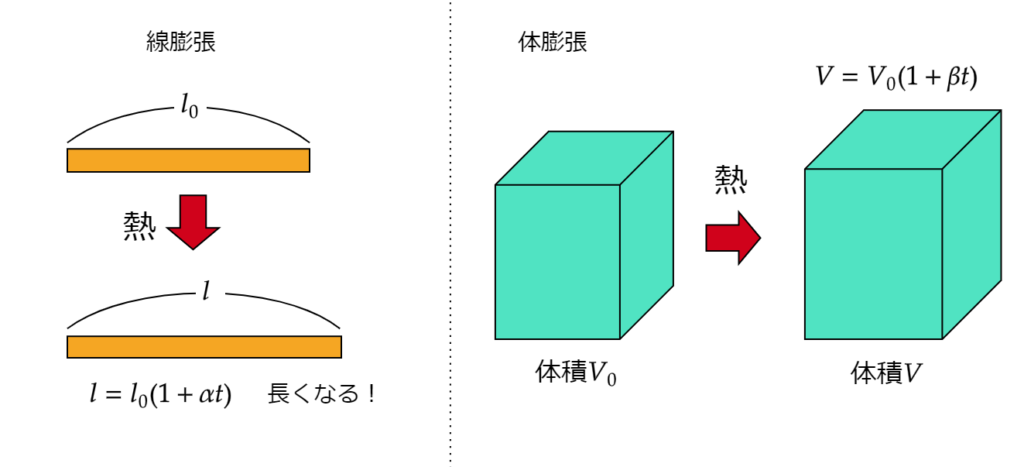
線膨張、体膨張の式は以下のとおりであり、\(\alpha , \beta \) は物質によって決まっている定数です。
$$l=l_0(1+\alpha t) , V=V_0(1+\beta t)\tag{2}$$
受験にはあまり出ませんね…。
ボイルシャルルの法則
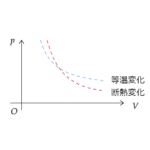
まずボイルの法則について説明します。(constは一定を意味します)
$$pV=\mathrm{const}\tag{3}$$
「温度が一定のとき一定量の気体の体積 \(V\) は気体の圧力 \(p\) に反比例する」というものです。
次にシャルルの法則を紹介します。
$$\frac{V}{T}=\mathrm{const}\tag{4}$$
「圧力が一定のとき、一定量の気体の体積 \(V\) は絶対温度\(T\) に比例する」というものです。
この2つを組み合わせます。
$$\frac{pV}{T}=\mathrm{const}\tag{5}$$
これがボイルシャルルの法則です。
理想気体の状態方程式
理想気体の状態方程式は
$$pV=nRT\tag{6}$$
で表されます。(\(n\) は物質量、 \(R\) は気体定数、 \(T\) は絶対温度)
ここで出てきた物質量 \(n\) は今考えている物質が何モルあるかを表します。
1モルは「\(6.02\times10^{23}\)個の原子やイオンなどの集団」のことを指します。
原子やイオンなどが\(6.02\times10^{23}\)個ある=1モル存在するということです。
3モル=原子やイオンが\(18.06\times10^{23}\)個あるということになります。
突然出てきた気体定数 \(R\) は
$$R=\frac{1.013\times 10^5\times 2.24\times10^{-2}}{273}=8.31 \mathrm{[J/(mol\cdot K)]}\tag{7}$$
で表されます。
問題
問題です。
2モルの水素が27°C、体積 \(3\times 10^{-2} \mathrm{[m^3]}\) の箱に詰まっているとします。
気体定数 \(R=8.3 \mathrm{J/mol\cdot K}\) とするとき圧力はいくつでしょうか?
では答えです。
状態方程式を立てます。
$$PV=nRT$$
より
$$P=\frac{nRT}{V}$$
$$P=\frac{2\times 8.3\times (273+23)}{3 \times 10^{-2}}$$
$$P=1.66\times 10^5 \mathrm{[Pa]}$$
となります!
まとめ
今回は熱力学の序論である熱と理想気体の状態方程式について学びました。
熱と温度では用語をしっかりと覚えることが重要で、後半は理想気体の状態方程式は問題演習を通してしっかりと身につけましょう!
次はこちら!2-2気体の分子運動論