ここからは磁場の話が出てきます。
磁気と電気は似ていますが、異なるところも多いので気を付けてください。
静磁場
空間に磁石を置くとその周りに磁場が発生します。
とくに、磁場が時間に依存しない場合を静磁場といいます。
磁石にはN極とS極があります。
一般的に磁場の向きはN極をプラス、S極をマイナスとして考えることが多いです。
静磁場と電流
電気と磁気は切っても切れない関係にあります。
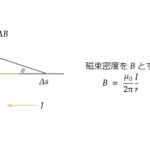
磁場中に導線を置き、電流を流すとその導線は力を受けます。
このとき、導線と磁場とのなす角を \(\theta\) とすると、導線の長さ \(\Delta s\) の部分に働く力 \(\Delta F\) は
$$\Delta F = IB\sin\theta \cdot \Delta s$$
になります。
今スカラー量で書きましたがこれをベクトル表記にしてみます。すると
$$\Delta \vec{F} = (\vec{I}\times \vec{B})\Delta s$$
となります。
この向き…わかりますか?
中学生の時に習ったフレミングの左手の法則がまさにこれです。
親指、人差し指、中指を直角になるように伸ばしたとき、中指が電流の向き、人差し指が磁場の向き、そして親指が力の向きを表す、というやつです。
突然出てきた \(B\) は磁束密度です。
電場のときに電束密度 \(D\) というものが出てきましたよね。
$$D = \epsilon_0 E$$
これと同じように、磁場の強さ \(H\) と磁束密度 \(B\) には次のような関係が成り立ちます。
$$H = \frac{1}{\mu_0}B $$
これは後程紹介するビオ-サバールの法則から導くことができます。
上記2つの式の形から \(E\) と \(B\) 、 \(D\) と \(H\) には対応関係があります。
\(E\) と \(B\) は場の中に置いた荷電粒子に働く力によって定義されている一方、 \(D\) と \(H\) は電荷密度、電流密度と関係しています。
今は E-B 対応の説明をしましたが、人によっては E-H 対応で話を進める場合もあるんですよ。
(この対応はややこしいので気を付けてください… 使用している教科書があれば、必ずどちらの形式で書いてあるかを確認してくださいね。)
荷電粒子に働く力
先ほどの式をもう一度載せます。
$$\Delta \vec{F} = (\vec{I}\times \vec{B})\Delta s$$
導線の断面積を \(S\) として、電流密度を使って表してみます。すると
$$\Delta \vec{F} = (\frac{\vec{i}}{S}\times \vec{B})\Delta s$$
となります。
両辺を \(S\Delta s\) で割ります。
単位体積当たりに働く力を \(f\) とすると
$$f = \vec{i}\times \vec{B}$$
が出てきます。電流を書き換えると次のようになります。
$$f = -ne\vec{v}\times \vec{B}$$
電子を一つとすると電子の数密度 \(n\) はこの式から取り除くことができ、電子 \(-e\) を電荷 \(q\) に置き換えると
$$F = q\vec{v}\times \vec{B}$$
となります。これがローレンツ力です。
今は磁場がかかっているときのみを考えましたが、電場を加えると次のようになります。
$$\vec{F} =q\vec{E} + q\vec{v}\times \vec{B}$$
これが電場と磁場が印加した時、電荷に加わる力です。
まとめ
今回は静磁場を取り扱いました。
ローレンツ力、フレミングの法則などは超重要ですので絶対に覚えてください!