
電磁誘導の法則を学んでいきます。
今までは静電場、静磁場について勉強しましたが、ここからは時間変化を伴うパターンを見ていきます。
電磁誘導
電磁誘導
ファラデーは一つ目の閉回路に電流を流した瞬間、その隣にある閉回路にも電流が流れるということを発見しました。
また、電源を切った瞬間にも流れます。
電流が時間変化するときに磁場が発生するので、このことから磁石を近づけたり遠ざけたりするときに電流が流れることが分かりました。
これを電磁誘導と呼びます。
ここからは電磁誘導がよく出てくるので忘れないようにして下さい
磁束
よく出てくる磁場 \(B\) は磁束密度とも呼ばれます。
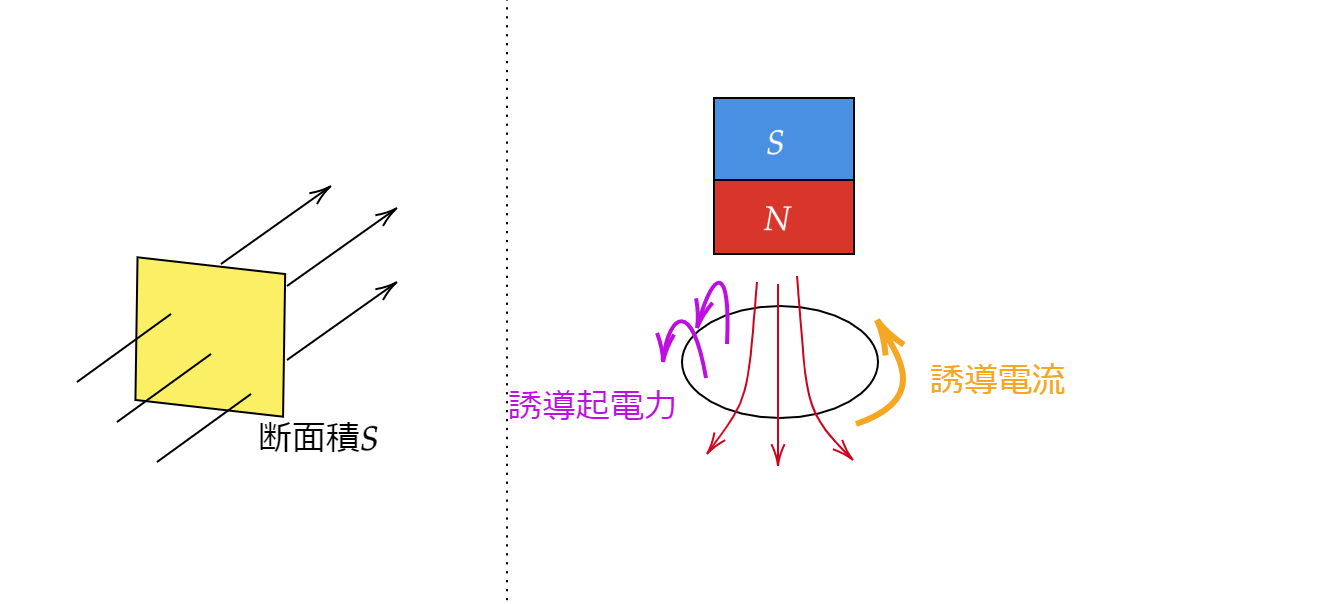
面積 \(S\) の平面上の回路に、一様な磁場が垂直にかかっている場合を考えます。
この磁束密度 \(B\) と、面積 \(S\) をかけると磁束 \(\Phi\) が出てきます。
$$\Phi = BS$$
シンプルな関係式ですね。
磁場が変化したときに流れる電流を起電力といい、よく \(\Phi_{em}\) であらわします。
この起電力の向きに気を付けてください。
起電力の向きは回路に流れる電流が作り出す磁場を弱めあう向きです。
数式上ではマイナスを付けます。磁束を時間で微分すればよくて
$$\Phi_{em} = -k\frac{d\Phi}{dt}$$
kは適当は比例係数です。(ただしk>0)
電流が流れている閉回路に磁石を近づけるときは図のように磁束を弱める向きに電流が流れます。(レンツの法則と右ねじの法則を思い出してください)
回路が平面でなく、磁束密度が場所に関係ないときは
$$\Phi = \int \vec{B}\cdot \vec{n} dS$$
で表されます。曲面に裏から表に向きになっている法線ベクトルを \(n\) としました。
静磁場中を運動する回路
次は磁束密度が変化するのではなくて電流が流れているまっすぐな導線が静磁場中を動くパターンを考えてみます。
電流が流れるということは電荷が流れているということですのでまずは電荷に注目します。
電荷を \(-e\) とすると、ローレンツ力の考え方から
$$\vec{F} = -e\vec{v}\times \vec{B}$$
です。 \(v\) は電荷の速度です。
導線が有限の長さの時は最終的に電荷が端に流れ着き、平衡状態に達してしまいます。
では導線がまっすぐではなく長方形で閉じている場合を考えます。
このとき、導線を動かしても磁場が一定であれば電流は流れません。
なぜならBCとADに電子があるとき、電子に働く力は大きさが等しく、逆向きになるため打ち消しあうからです。
では磁場が一様ではないときはどうでしょうか?
その場合、BC間にある電子に働く電位差は \(\phi_1 = vB_1l\), AD間は\(\phi_2 = vB_2l\) です。(ただし \(l\) は導線の長さです。)
よって回路上に生じる起電力 \(\phi_{em}\) は
$$\phi_{em} = -\phi_1+\phi_2 = -(B_1-B_2)av$$
となります。
導線が動く前と動いた後の磁束の変化量は
$$\Delta \Phi = B_1av\Delta t-B_2av\Delta t = (B_1-B_2)av\Delta t$$
先ほど導出した \(\phi_{em}\) と等しく、 \(\Delta t->0\) の極限を考えると
$$\Phi_{em} = -\frac{d\Phi}{dt}$$
になります。
ファラデーの電磁誘導の法則
電磁誘導の法則についてまとめます。
磁場が時間に依存して変化した時、起電力は次のように表せます。
$$\phi_{em} = \int{E\cdot t}ds$$
\(t\) は回路に沿った単位ベクトルです。
そして起電力は磁束の時間微分にマイナスを付けたもので表せるので
$$\phi_{em} = \int{E\cdot t}ds = -\frac{d\Phi}{dt}$$
となります。
磁束は磁場とそれを貫く面積都の積で表せましたので
$$-\frac{d\Phi}{dt} = -\frac{\partial B}{\partial t}\cdot n\Delta S$$
左辺は渦なしの法則の微分形から回転の形で表せます
$$\int{E\cdot t}ds = \int \nabla \times E dS$$
これらをまとめたものがファラデーの電磁誘導の法則です。
$$ \nabla \times E = -\frac{\partial B}{\partial t}$$
これで磁場と電場が一つの式にまとまりました。
磁場が時間変化すると電場が発生することがこの式からわかります。
まとめ
今回は電磁誘導の基礎を勉強しました。
電場と磁場が結びつく式がファラデーの電磁誘導の法則です。
忘れないようにしましょう!








