このページでは高校熱力学の公式・用語をまとめてみました。
確認用にぜひお使いください!
全体概要
当サイトでは熱力学の分野を以下の4つに分けています。
公式集
ボイルシャルルの法則・理想気体の状態方程式・熱力学の第一法則あたりがメインになります。
しかし線膨張やマイヤーの法則などもしっかり覚えましょう!
(constは「一定」の意味です)
| 用語・名前 | 公式 | 説明 |
| 絶対温度 | $$T=t+273.15$$ | ケルビン[K]で表される温度 |
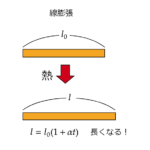
| 線膨張 | $$l=l_0(1+\alpha t)$$ | アルファ[\(\alpha\)]は物質によって決まっている定数 |
| ボイルの法則 | $$pV=\mathrm{const}$$ | 温度が一定のとき気体の圧力 p は絶対温度Tに反比例する |
| シャルルの法則 | $$\frac{V}{T}=\mathrm{const}$$ | 圧力が一定のとき気体の体積 V は絶対温度Tに比例する |
| ボイルシャルルの法則 | $$\frac{pV}{T}=\mathrm{const}$$ | 気体の体積 V は絶対温度Tに比例し、圧力 p に反比例する |
| 理想気体の状態方程式 | $$pV=nRT$$ | 理想的な気体が従う方程式 |
| ボルツマン定数 | $$k=\frac{R}{N_A}$$ | 気体定数 R ÷アボガドロ定数。その値は \(1.38\times10^{-23}\)[J/K]\) |
| 内部エネルギー | $$U=\frac{3}{2}nRT$$ | 気体分子の熱エネルギーと分子間に働く位置エネルギーの総和のこと |
| 熱力学の第一法則 | $$\Delta U=Q+W$$ | Q は気体に入る熱量。W は外部からされる仕事。それらの和が内部エネルギーの増加量になる |
| 定積変化時の内部エネルギー | $$\Delta U=Q$$ | 定積であるため、仕事はゼロとなる |
| 定圧変化時の内部エネルギー | $$\Delta U=Q-p\Delta V$$ | 説明は特にないですね |
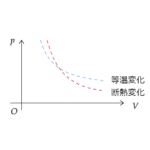
| 等温変化時の内部エネルギー | $$Q=-W$$ | 内部エネルギーは温度に依存するため、等温変化時にはゼロになる |
| 断熱変化時の内部エネルギー | $$\Delta U=W$$ | Q は入ってきた熱量を表すため、断熱時にはもちろんゼロとなる |
| 定積モル比熱・定圧モル比熱 | $$C_V=\frac{3}{2}R$$$$C_p=\frac{5}{2}R$$ | モル比熱とは 1molの物質の温度を 1K上昇させるのに必要な熱量のことです。これは単原子分子の場合で、2原子分子の場合は+1されます。(入試ではほぼ出ない?) |
| マイヤーの法則 | $$C_p=C_V+R$$ | そのままです。導出は大学で習います |
| ポアソンの式 | $$pV^\gamma=const$$ | 断熱変化における圧力と体積の関係。単原子分子の場合 \(\gamma=C_p/C_V\)は 5/3 となる |
| 熱効率 | $$e=W/Q$$ | 熱エネルギーをどのくらい仕事に変換できるかを表す。1は超えません |
内部エネルギーはまとめられるのでもっと少なくなります。
この下にもっとコンパクトにしたものを載せておきました。
公式集(最小限)
まとめられるものをまとめてみました。
| 用語・名前 | 公式 | 説明 |
| 絶対温度 | $$T=t+273.15$$ | ケルビン[K]で表される温度 |
| 線膨張 | $$l=l_0(1+\alpha t)$$ | アルファ[\(\alpha\)]は物質によって決まっている定数 |
| ボイルシャルルの法則 | $$\frac{pV}{T}=const$$ | 気体の体積 V は絶対温度Tに比例し、圧力 p に反比例する |
| 理想気体の状態方程式 | $$pV=nRT$$ | 理想的な気体が従う方程式 |
| ボルツマン定数 | $$k=\frac{R}{N_A}$$ | 気体定数 R ÷アボガドロ定数。その値は \(1.38\times10^{-23}\)[J/K]\) |
| 内部エネルギー | $$U=\frac{3}{2}nRT$$ | 気体分子の熱エネルギーと分子間に働く位置エネルギーの総和のこと |
| 熱力学の第一法則 | $$\Delta U=Q+W$$ | Q は気体に入る熱量。W は外部からされる仕事。それらの和が内部エネルギーの増加量になる |
| 定積モル比熱・定圧モル比熱 | $$C_V=\frac{3}{2}R$$$$C_p=\frac{5}{2}R$$ | モル比熱とは1molの物質の温度を1K上昇させるのに必要な熱量のことです。これは単原子分子の場合で、2原子分子の場合は+1されます。(入試ではほぼ出ない?) |
| マイヤーの法則 | $$C_p=C_V+R$$ | そのままです。導出は大学で習います |
| ポアソンの式 | $$pV^\gamma=const$$ | 断熱変化における圧力と体積の関係。単原子分子の場合 \(\gamma=C_p/C_V\) は5/3となる |
| 熱効率 | $$e=W/Q$$ | 熱エネルギーをどのくらい仕事に変換できるかを表す。1は超えない |
少ないですね…。
あくまでこの記事は復習用です。
公式を覚えるだけでは入試問題は解けません。問題演習を通してしっかり公式の意味と使い方を理解しましょう!
用語集
だいたい「熱」か「変化」という言葉が入っています。
惑わないように気を付けましょう!
| 用語 | 説明 |
| 熱運動 | 原子や分子が行う無秩序な運動のこと |
| 絶対温度 | 全ての物質が凍る温度をゼロとした時の温度 \(T=t+273.15\) |
| 熱平衡 | 高温の物体と低温の物体を接触させたとき、2つの物体の温度が等しくなること |
| 熱 | 物体間で移動する熱運動のエネルギー |
| 線膨張・体膨張 | 熱を加えると物体が膨張すること |
| 線膨張率・体膨張率 | 物質によって決まっている定数です。大きければ温度を高くしたとき、より膨張すること |
| 気体の内部エネルギー | 熱運動による運動エネルギーと分子間に働く力による位置エネルギーの総和 |
| 熱力学の第一法則 | 気体の内部エネルギーは気体の入る熱量と外部からされる仕事の和で表される |
| 定積変化 | 体積を一定にして温度や圧力などを変化させること |
| 定圧変化 | 圧力を一定にして温度や体積などを変化させること |
| 等温変化 | 温度を一定にして圧力や体積などを変化させること |
| 断熱変化 | 外部との熱のやり取りを遮断しして圧力などを変化させること |
| モル比熱 | 1[mol]の物質を1[K]上昇させるのに必要な熱量のこと |
| 熱機関 | 熱を仕事に変える装置のこと |
| 熱効率 | 高温の熱源から得られた熱と外部へした仕事の割合 |
| 不可逆変化 | 自然には元に戻せない変化のこと |
| 熱力学の第二法則 | 1つの熱源から熱を得て、それをすべて仕事に変えることのできる機関は存在しない |
| 第一種永久機関 | 外部からエネルギーをもらわずに仕事をし続ける機関のこと |
| 第二種永久機関 | 熱効率 e が1である機関のこと |
「○○変化」はそのままなので省略しても大丈夫かなと思いましたが一応ひととおり書きました。
20個くらいなので頑張れば一日で覚えられるかも…?
まとめ
5分野ある中で「熱分野」は一番公式、用語が少ない分野です。
是非マスターしましょう!