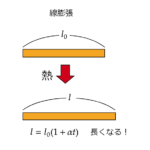
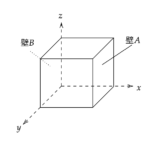
前回はこちら!2-2気体の分子運動論
ここでは内部エネルギーについて学びます。
力学でエネルギーに注目することがありましたよね?この熱分野でも同様にエネルギーに注目します。
さらに温度が等しい場合、物体の内部と外部の熱のやり取りを考えないときなどを考えます。
気体の内部エネルギー
力学分野で力学的エネルギーという用語があったかと思います。
これは確か「運動エネルギー」+「位置エネルギー」でしたね。
熱力学にも似たような言葉で気体の内部エネルギーという用語があります。
これは熱運動による運動エネルギーと、ファンデルワールス力などの分子間に働く力による位置エネルギーの総和です。
しかし、ここからも同様、ファンデルワールス力などの相互作用を無視した理想気体を取り扱います。そのため
気体の内部エネルギー=分子の運動エネルギーの和
になります。
また、ここではアルゴンや炭素などの単原子分子を扱います。窒素や酸素などの二原子分子では内部エネルギー、モル比熱の値が少し変わります。頭の片隅にでも入れておいてください。
さて、気体の内部エネルギー=分子の運動エネルギーの総和でしたので内部エネルギーUは以下の通りになります。
$$U=\frac{1}{2}m\bar{v^2}\times nN_A\tag{1}$$
これは運動エネルギー×分子の数です。ここで前回出てきた
$$\frac{1}{2}m\bar{v^2}=\frac{3R}{2N_A}T\tag{2}$$
を利用すると次式が得られます。
$$U=\frac{3}{2}nRT\tag{3}$$
ここで出てきた \(n\)[mol]は物質量、\(N_A\) はアボガドロ定数です。
なお、絶対温度を \(\Delta T\) だけ変化させるとき、内部エネルギーの変化量は
$$\Delta U=\frac{3}{2}nR(T+\Delta T)-\frac{3}{2}nRT=\frac{3}{2}nR\Delta T\tag{4}$$
になります。
\(n\) は物質量、\(R\) は気体定数ですので内部エネルギーは温度に依存することが分かります。
熱力学の第一法則
気体の内部エネルギーの増加量は
$$\Delta U=Q+W\tag{5}$$
で表されるのが熱力学の第一法則です。日本語で説明すると
気体の内部エネルギーの変化量[J]=気体に入る熱量Q[J]+気体が外部からされる仕事W[J]
になります。
気体が外部からされる仕事 \(W\) は圧力 \(p\) ×気体の体積の変化量 \(\Delta V\)で表されることが多いです。
圧力に面積をかけると力になりますよね。よって
$$W=F\Delta l=pS\Delta l=p\Delta V\tag{6}$$
これを式(5)に代入すると
$$\Delta U=Q+p\Delta V\tag{7}$$
になります。以下こちらの(7)式を使います。
気体の状態変化
今出てきた熱力学の第一法則を利用して、入試には「温度を一定にして変化させた」や「外部との熱を遮断して~」などの表現が問題文に出てきます。
その時には「これは等温変化の話だな」「つまり断熱変化させているから、~のように考えればいいんだな」とできるようになりましょう!
定積変化
気体の体積を一定にして加熱、冷却をして温度を変えることを定積変化といいます。
熱力学の第一法則
$$U=Q+p\Delta V\tag{7}$$
において「定積」である場合を考えましょう。
右辺第二項は体積の変化量を表しています。しかし、今考えたいのは「定積」ですのでこの値はゼロになります。よって
$$\Delta U=Q\tag{8}$$
になります。すなわち、外部から得られた熱量=気体の内部エネルギーの総和になります。
定圧変化
気体の圧力を一定に保ちながら加熱、または冷却をして温度変化させることを定圧変化といいます。
この場合熱力学の第一法則は変わりません。
$$U=Q+p\Delta V\tag{9}$$
等温変化
気体の温度を一定に保ちながら気体の圧力や体積を変えることを等温変化といいます。
気体の内部エネルギーは式(5)を再び出すと
$$\Delta U=\frac{3}{2}nR\Delta T\tag{10}$$
\(n\) は気体によって決まっている量で、気体定数は定数です。そのため、等温、つまり温度の変化量がゼロの時、内部エネルギーもゼロになります。
したがって
$$0=Q+p\Delta V\tag{11}$$
$$Q=-W\tag{12}$$
となります。
断熱変化
外部と熱のやり取りを遮断することを断熱変化といいます。
今まで出てきた熱量 \(Q\) をゼロとすればよいので
$$U=0+p\Delta V\tag{13}$$
したがって
$$\Delta U=W\tag{14}$$
となります。
モル比熱
1[mol]の物質を1[K]上昇させるのに必要な熱量をモル比熱といいます。
定積モル比熱とは定積変化におけるモル比熱のことを指します。
定積モル比熱
定積モル比熱を \(C_V\) [/\J(mol\cdot K\)]で表すことが多いです。定積におけるモル比熱は
$$Q=nC_V\Delta T\tag{15}$$
定積ですので内部エネルギーの変化量は熱量に等しくなります。
$$\Delta U=nC_V\Delta T\tag{16}$$
になります。よって式(10)から定積モル比熱の値は
$$C_V=\frac{3}{2}R\tag{17}$$
となります。
定圧モル比熱
一つ上で説明した定積モル比熱と同じ流れです。熱量 \(Q\) は
$$Q=nC_p\Delta T\tag{18}$$
理想気体の状態方程式から
$$p\Delta V=nR\Delta T\tag{19}$$
が成り立つので
$$C_p=\frac{5}{2}R\tag{20}$$
です。ここで以下の関係が成り立ちます。
$$C_p=C_V=R\tag{21}$$
これをマイヤーの関係といいます。
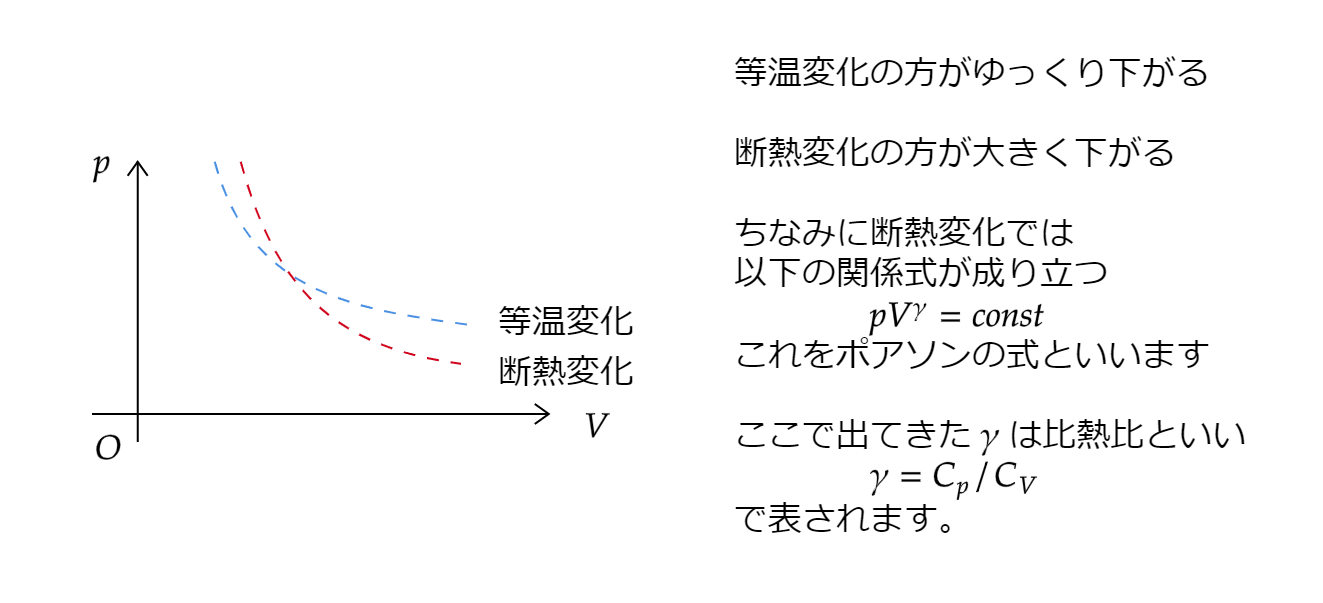
ちなみにポアソンの式を簡単に説明すると以下の通りです。
レベルの高い大学は出してきます。
まとめ
今回は内部エネルギーについて学びました。
様々な状況について考えましたが熱力学の第一法則さえ覚えていれば何とかなる場合が多いです。
また、比熱は定義をしっかり覚えましょう!
次はこちら!2-4熱効率・カルノーサイクル