前回はこちら!
電磁気分野最後の砦である交流について学びましょう!
交流
交流とは電流や電圧の向きが周期的に変化する電流のことを言います。
直流との相違点に注意しながら学習しましょう!
交流と抵抗
\(V=V_0\sin\omega t\) で表される交流電圧を抵抗 \(R\) に加えます。
交流電圧の正負を考えないとき、電流 \(I\) は次のようになります。
$$I = \frac{V}{R} = \frac{V_0}{R}\sin\omega t = I_0\sin\omega t$$
電圧がsinですので、電流も同じく振動します。
ここで大事なのは電流と電圧が同位相であるということです。
先に書いておきますが、コンデンサーとコイルの場合は同位相ではないです。
実効値
さて、抵抗で消費される電力はどうなるのでしょうか?
電力の時間平均は次の式で表されます。
$$\bar{P}=\frac{1}{2}V_0I_0$$
また、実効値というものを考えれば次のように扱えます。
$$\bar{P}=V_eI_e=RI_0^2=\frac{V_e^2}{R}$$
$$V_e\times \sqrt{2}=V_0$$
eという添え字が付いているものを実効値といいます。
この実効値を用いると電力は直流のときと同じように表せます。
一般的に交流電圧、電流は実効値を用いて表されることが多いです。
交流とコイル
自己インダクタンス \(L\) のコイルに同じく \(V=V_0\sin\omega t\) の電圧を加えます。
この時にコイルには電流の変化を妨げる向きに自己誘電起電力が働きます。
この起電力は
$$-L\frac{\Delta I}{\Delta t}$$
で表されます。このとき電流は次のように表されます。
$$I=-\frac{V_0}{\omega L}\cos\omega t=\frac{V_0}{\omega L}\sin(\omega t-\frac{\pi}{2})=I_0\sin(\omega t-\frac{\pi}{2})$$
(本当は微分をすれば分かりやすいのですが高校物理では取り扱わないのでここでは省略します。)
なお、電流の位相は電圧よりも \(\frac{\pi}{2}\) 遅れることになります。
先ほど出てきた \(\omega L\) をコイルのリアクタンスといいます。
リアクタンスとは交流が流れているときの抵抗のようなものです。
交流とコンデンサー
コンデンサーを交流回路につなげた時充電と放電を繰り返します。
コイルと同様な電圧が流れているとしましょう。\(V=V_0\sin\omega t\) の電圧を加えます。
この時にコンデンサーによる電位差は
$$Q=CV=CV_0\sin\omega t$$
で表されます。このとき電流は次のように表されます。
$$I=\omega CV_0\cos\omega t=\omega CV_0\sin(\omega t+\frac{\pi}{2})=I_0\sin(\omega t+\frac{\pi}{2})$$
(本当は積分をすれば分かりやすいのですが高校物理では取り扱わないのでここでも省略します。)
なお、電流の位相は電圧よりも \(\frac{\pi}{2}\) 進んでいることになります。
そして\(\frac{1}{\omega C}\) をコンデンサーのリアクタンスといいます。
これもコイルのリアクタンスと同様に交流に対して抵抗に相当する働きを持ちます。
RLC直列回路
抵抗、コイル、コンデンサーの3つを直列につなげた回路を考えます。
先ほどは電圧を基準にしてそれより電流が遅れているか進んでいるかを考えましたが、今回は電流を基準に考えてみましょう。
そのためコイルの場合、電流に比べ電圧の位相が進んでいます。
逆にコンデンサーの電圧の位相は電流に比べ遅れています。
そのことを頭に入れると次の式が出てきます。
$$V_0 = RI_0\sin(\omega t)$$
$$V_L = \omega LI_0\sin(\omega t+\frac{\pi}{2}) = \omega LI_0\cos(\omega t)$$
$$V_C = \frac{I_0}{\omega C}\sin(\omega t-\frac{\pi}{2}) = \frac{I_0}{\omega C}\cos(\omega t)$$
キルヒホッフの第二法則よりこれらを一気にまとめちゃいます。
$$V_0 = RI_0\sin(\omega t) + (\omega L – \frac{1}{\omega C})I_0\cos(\omega t) $$
$$=\sqrt{R^2 + (\omega L – \frac{1}{\omega C})^2}I_0\sin(\omega t + \alpha)$$
はいできました。
最後に出てきた \(\alpha\) は電圧と電流の位相差を示しています。
そのまえの \(\sqrt{R^2 + (\omega L – \frac{1}{\omega C})^2}\) はインピーダンスと呼ばれ、抵抗に相当する働きを持ちます。
共振回路
共振回路とは先ほどのRLC直列回路において
\(\omega L-\frac{1}{\omega C}\) の部分が0になるときインピーダンスが最小となり、 \(I_0\) が最大になります。これを共振といいます。
共振時の角周波数は共振角周波数といい、以下のように与えられます。
$$\omega_0 = \frac{1}{LC}$$
また、このときの周波数を共振周波数といい、以下のようにあらわせます。
$$f_0 = \frac{\omega_0}{2\pi} = \frac{1}{2\pi\sqrt{LC}}$$
電磁波
最後に電磁波を勉強しましょう。
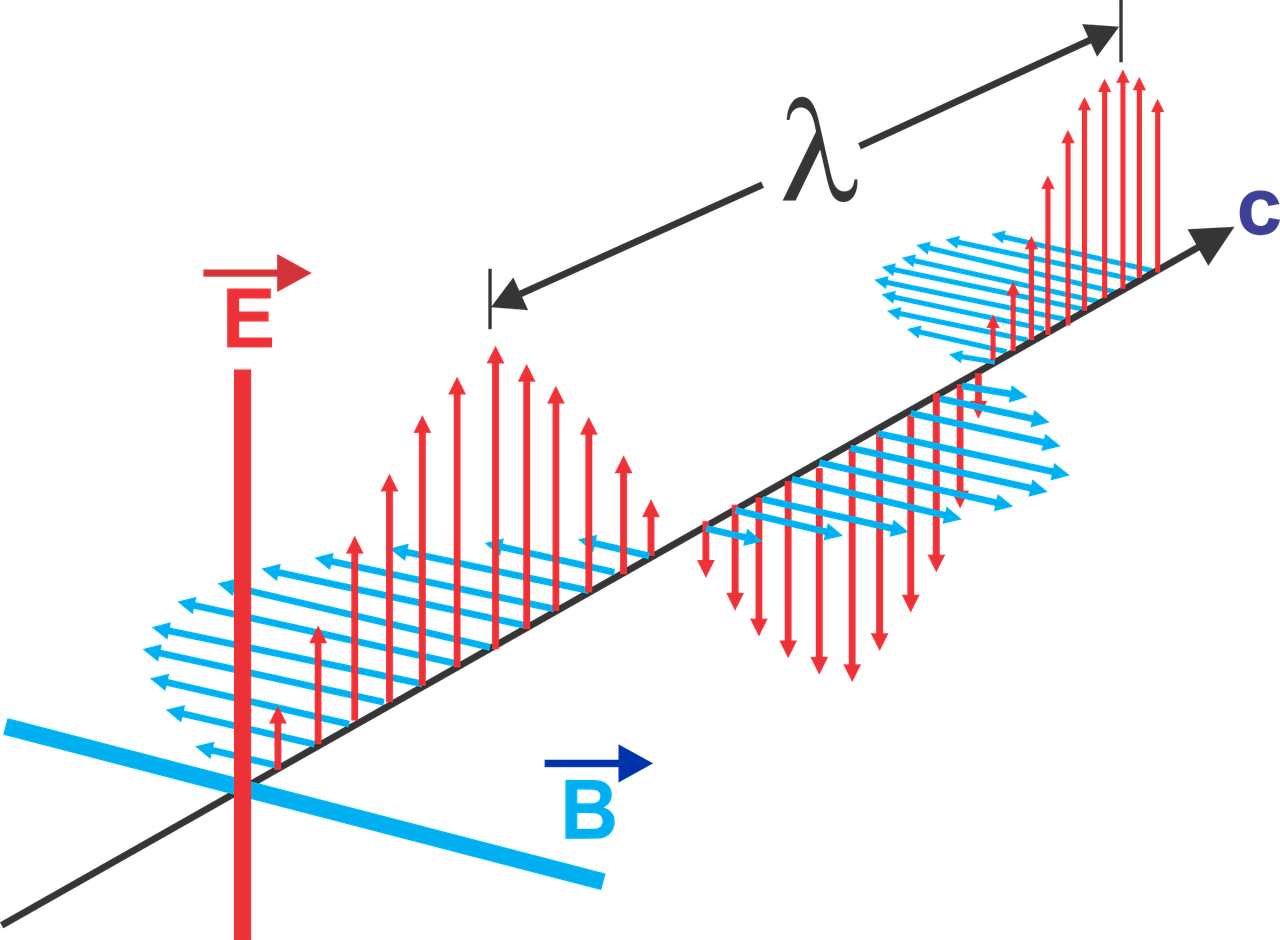
電磁波はその名の通り電場と磁場による波です。
変化する磁場の周りに電場が生じますし、変化する電場の周りに磁場が生じます。
このことから電場と磁場が繰り返し発生することが分かります。電磁波はこのようにしてできます。
受験ではあまり出ませんね…
電磁波はもちろん波ですから反射や屈折、回折や干渉も起こります。
知識として覚えておきましょう!
まとめ
RLC回路はよく出てきますのしっかりとマスターしましょう!
次はこちら!