前回はこちら!
今回は電磁誘導について説明します。
何がどうなっているかわかりにくくなるのでしっかりと区別しながら進みましょう!
電磁誘導
まずは電磁誘導について説明します。
コイルを貫く磁場が時間とともに変化するとき、コイルに電流が流れます。
電流が流れると起電力が生じます。
この現象のことを電磁誘導と呼び、発生する起電力を誘導起電力といいます。
さらにこの流れている電流を誘導電流と呼びます。
磁束
前回、磁束密度 \(B\) が出てきましたが、磁束の説明をしていませんでした。
磁束密度 \(B\) に対して垂直な断面積 \(S\) があるとします。このとき
$$\Phi=BS$$
という式が成り立ちます。
\(\Phi\) は「ファイ」と読み、これが磁束です。
磁束 \(\phi\) は断面積を貫く磁束線の本数を表しています。
磁束の単位は [Wb] ウェーバが使われます。
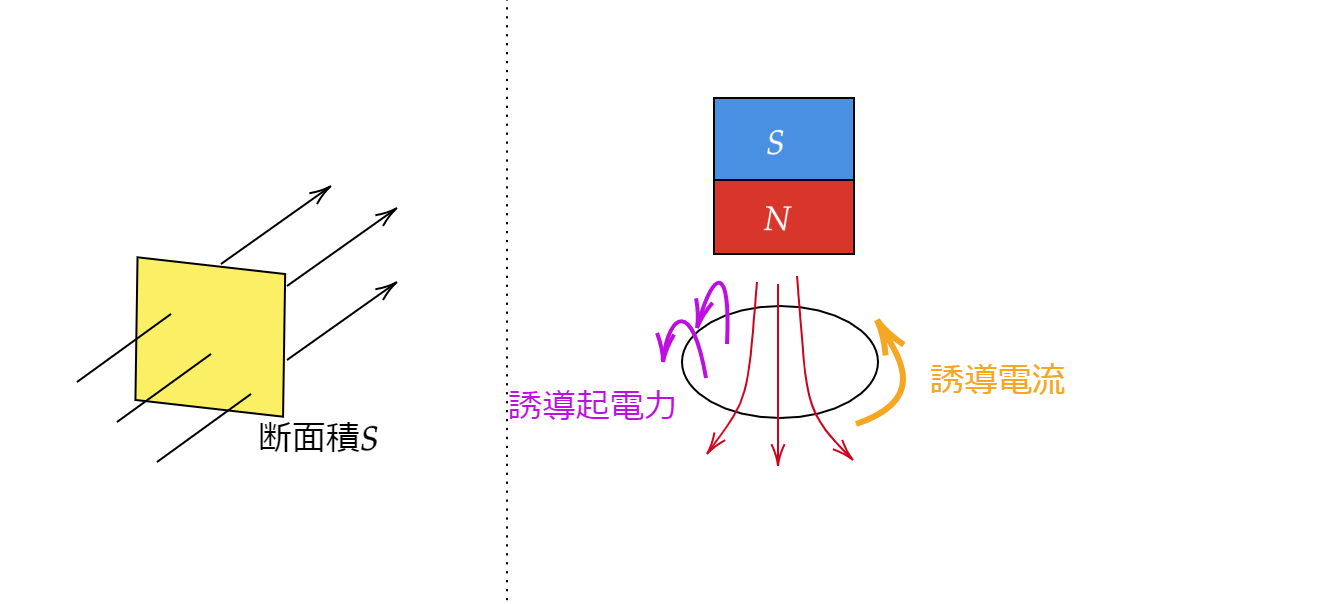
レンツの法則とファラデーの電磁誘導
レンツの法則を覚えましょう
コイルを貫く磁束の変化を妨げる向きに誘導起電力が生じる。
というものです。
何を言っているのか文だけではわかりにくいので図で確認しましょう。
さらに誘導起電力の大きさはコイルを貫く磁束の単位時間当たりの変化量に比例します。
これとレンツの法則を合わせてファラデーの電磁誘導の法則と呼びます。
(「単位時間あたり」は「1秒間に」という意味だと思って大丈夫です。)
これを式にしてみましょう
$$V=-\frac{\Delta \Phi}{\Delta t}$$
\(V\) は誘導起電力で単位はボルト [V] 、分子は上で説明した磁束で、分母は時間です。
時間の単位はもちろん [s] です。
磁場中を動く導体
入試でよく見かける気がします。
磁束密度が一様で鉛直上向きな磁場中に平行な導線を置きます。
それらの距離は \(l\) であるとします。
磁場に垂直な方向に速さ \(v\) で導体棒を動かすとき、ファラデーの電磁誘導の法則から
$$V=-\frac{\Delta \Phi}{\Delta t}=-\frac{\Delta BS}{\Delta t}=-\frac{\Delta B\times l v\Delta t}{\Delta t}$$
$$V=-vBl$$
マイナスが付いているので向きはレンツの法則より、磁場を弱めさせる向きに誘導電流が流れます。
自己誘電
自己誘電とはコイルを流れる電流を変化させると、コイルには電流の変化を妨げる向きに起電力が発生するというものです。
コイルに流れる電流が、\(\Delta t\)の間に \(\Delta I\) 変化するとコイルに起電力が生じます。その時次の式で表せます。
$$V=-L\frac{\Delta I}{\Delta t}$$
このとき出てきた \(L\) は自己インダクタンスといいます。その単位はヘンリーです。
1Hは電流が毎秒1Aの割合で増加するとき、1Vの誘電起電力が生じるコイルの自己インダクタンスといいます。
相互誘導
接近した2つのコイルにおいて片方のコイル1に流れる電流を変化させると、コイル2を貫く磁束も変化するのでコイル2にも誘電起電力が生じます。
これを相互作用といいます。
$$V_2=-M\frac{\Delta I_1}{\Delta t}$$
このときの \(M\) は相互インダクタンスと呼ばれる定数です。
単位は自己インダクタンスと同じくヘンリーです。
まとめ
今回は電磁誘導について学びました。
よく出てくるのでしっかりマスターしましょう!
次はこちら!