前回はこちら!2-1熱と温度・ボイルシャルル・理想気体の状態方程式
ここでは気体の圧力や温度といったマクロな物理量と気体の速さや質量などのミクロな物理量を関連付ける話をします。
誘導付きで入試に出ることがあります!
しっかりと理解しましょう!
気体の分子運動論
一辺の長さが \(l\) の立方体の容器内に質量 \(m\) の気体分子が \(N\) 個入っている状況を考えます。
ここで細かな条件を無視します。(容器の壁はなめらかで、気体分子は常に一定の速さで壁に弾性衝突をし、分子同士は衝突しないものとします。)
以下の図のようにx,y,z軸を取ります。x軸に垂直な壁Aが受ける圧力を求めましょう!
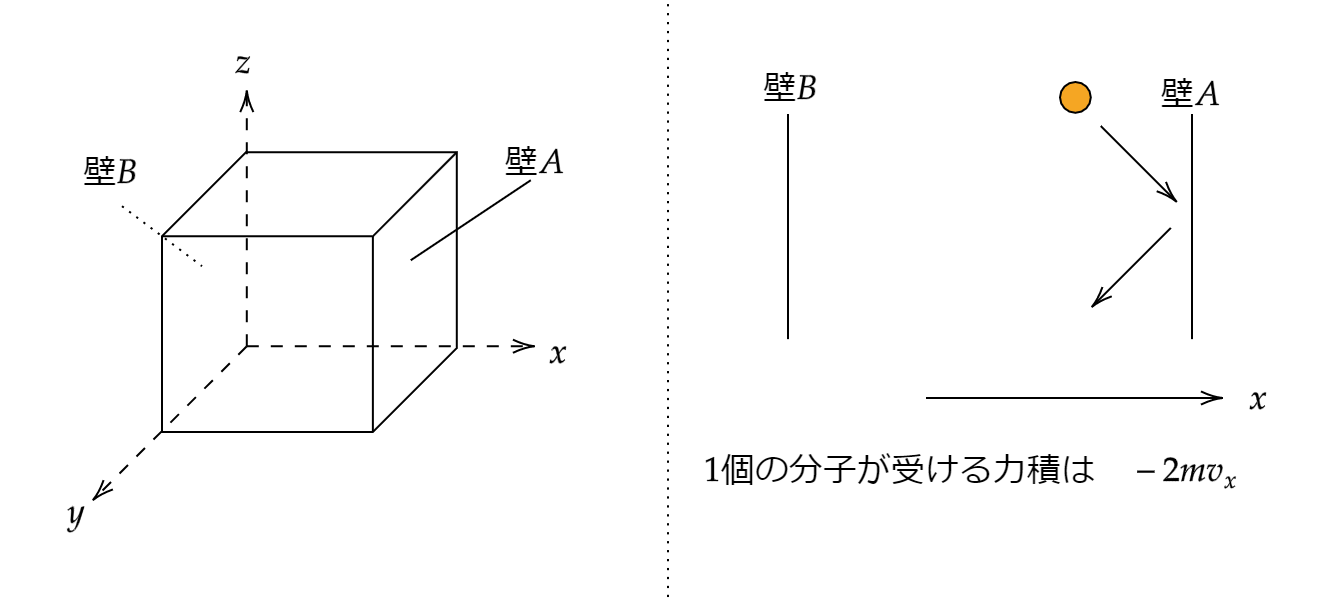
1個の分子が壁から受ける力積
1個の分子の速度を \(\vec{v}\)、x軸の速度成分を \(v_x\) として壁Aに衝突し、跳ね返る場合の力積を考えましょう。
弾性衝突し、分子の速度は衝突前後で変わらないと仮定しているため、1回の衝突による運動量の変化量は、
$$-mv_x-(mv_x)=-2mv_x\tag{1}$$
このようになります。気を付けてほしいのは今は1個の分子が壁Aから受ける力積を考えているため値がマイナスになっています。
x軸は右向きに正を取っていますよね。このとき、分子が受ける力積はマイナスになります。
作用反作用の法則から壁Aが受ける力積は \(2mv_x\) です。
分子1個が受ける平均の力
分子が壁Aに衝突した後、再び壁Aにぶつかるまでの時間を考えましょう。
立方体の1辺の長さが \(l\) だから距離は \(2l\) ですね。分子の x軸方向の速度は \(v_x\) であるため、時間 \(t_1\) は
$$v_x\times t_1=2l\tag{2}$$
$$t_1=\frac{2l}{v_x}\tag{3}$$
になります。
1往復する時間が分かったのでこの分子が \(t\) 秒間に壁に衝突する回数は
$$\frac{t}{2l/v_x}=\frac{v_xt}{2l}\tag{4}$$
です。左辺を日本語に直すと(壁に衝突する回数=時間 \(t\) / 1往復する時間)です。わかりにくいので具体的な数字を入れてみましょう。
1往復するのに6秒間かかるとしましょう。では30秒間に分子1個が壁に衝突する回数は何回でしょうか?
これは30÷6=5になりますよね。ということで5回です。
さて、壁Aが分子1個から受ける平均の力 \(\bar{f}\) を求めよう。
\(t\) 秒間に壁Aがこの分子から受ける力積は
$$\bar{f}t=2mv_x\times \frac{v_xt}{2l}=\frac{mv_x^2t}{l}\tag{5}$$
となる。つまり平均の力 \(\bar{f}\) は
$$\bar{f}=\frac{mv^2_x}{l}\tag{6}$$
となります。
N個の分子による圧力
N個の分子の平均速度を \(\bar{v_x^2}\) とすると \(\Sigma v_x^2=N\bar{v_x^2}\) となります。
N個の分子から受ける壁Aの力の総和 \(F\) は
$$F=\Sigma \bar{f}=\Sigma \frac{mv_x^2}{l}=\frac{Nm\bar{v_x^2}}{l}\tag{7}$$
壁Aが受ける圧力は(圧力=力÷面積より)
$$p=\frac{F}{l^2}=\frac{Nm\bar{v_x^2}}{l^3}=\frac{Nm\bar{v_x^2}}{V}\tag{8}$$
となります。ただし立方体の体積を \(V\) としました。
分子の速度は
$$v^2=v_x^2+v_y^2+v_z^2\tag{9}$$
という関係が成り立つので平均速度も同様に成り立ちます。
$$\bar{v^2}=\bar{v_x^2}+\bar{v_y^2}+\bar{v_z^2}\tag{10}$$
分子に速度の偏りはないため
$$\bar{v_x^2}=\bar{v_y^2}=\bar{v_z^2}\tag{11}$$
が成り立ちます。つまり
$$\bar{v^2}=\bar{v_x^2}+\bar{v_y^2}+\bar{v_z^2}=3\bar{v_x^2}\tag{12}$$
式\(8\)より
$$p=\frac{Nm\bar{v^2}}{3V}\tag{13}$$
ボルツマン定数
今度は気体の温度とミクロな分子運動と関係づけることができます。
容器内に気体 \(n\)[mol]あるとき、その分子の数は \(nN_A\) になります。
ここで出てきた \(N_A\) はアボガドロ定数です。
これを先ほどの\(13\)式、理想気体の状態方程式と比べると
$$pV=\frac{nN_Am\bar{v^2}}{3}\tag{14}$$
$$RT=\frac{N_Am\bar{v^2}}{3}\tag{15}$$
これを少し変形します。
$$\frac{N_Am\bar{v^2}}{3}=RT\tag{16}$$
$$m\bar{v^2}=\frac{3R}{N_A}T\tag{17}$$
ここで両辺に1/2をかけます。
$$\frac{1}{2}m\bar{v^2}=\frac{3R}{2N_A}T\tag{18}$$
ここで(18)式の左辺に注目してください。これは運動エネルギーの平均値を表していることになります。したがって
$$\frac{1}{2}m\bar{v^2}=\frac{3R}{2N_A}T=\frac{3}{2}k_BT\tag{19}$$
となります。ここで出てきた \(k_B\) はボルツマン定数と呼ばれていまして
$$k_B=R/N_A=1.38\times 10^{-23}\mathrm{[J/K]}\tag{20}$$
です。気体定数をアボガドロ定数で割れば出てきます。
最後に式(18)より質量 \(m\) を右辺に移項して
$$\bar{v^2}=\frac{3RT}{mN_A}\tag{21}$$
ここで両辺にルートを取りますと
$$\sqrt{\bar{v^2}}=\sqrt{\frac{3RT}{mN_A}}\tag{22}$$
これが気体分子の二乗平均速度と呼ばれます。
意味は言葉のままで、気体分子の平均の速度を表します。
まとめ
さて、今回は分子運動論を勉強しましました。
入試には誘導付きで出てくることがありますが、やり方が分かればそこまで難しくないので是非マスターしましょう!
次はこちら!2-3気体の内部エネルギー・比熱