前回はこちら!3-6レンズと鏡
ヤングの実験について説明します。
先に結論を言ってしまいますがこの実験の何がすごいのかといいますと、ヤングの実験によって光が波としての性質を持つことを示されました。
この画期的な実験は入試問題に良く出ます。誘導形式で出てくることもあります。
実験装置は以下の図の通りです。
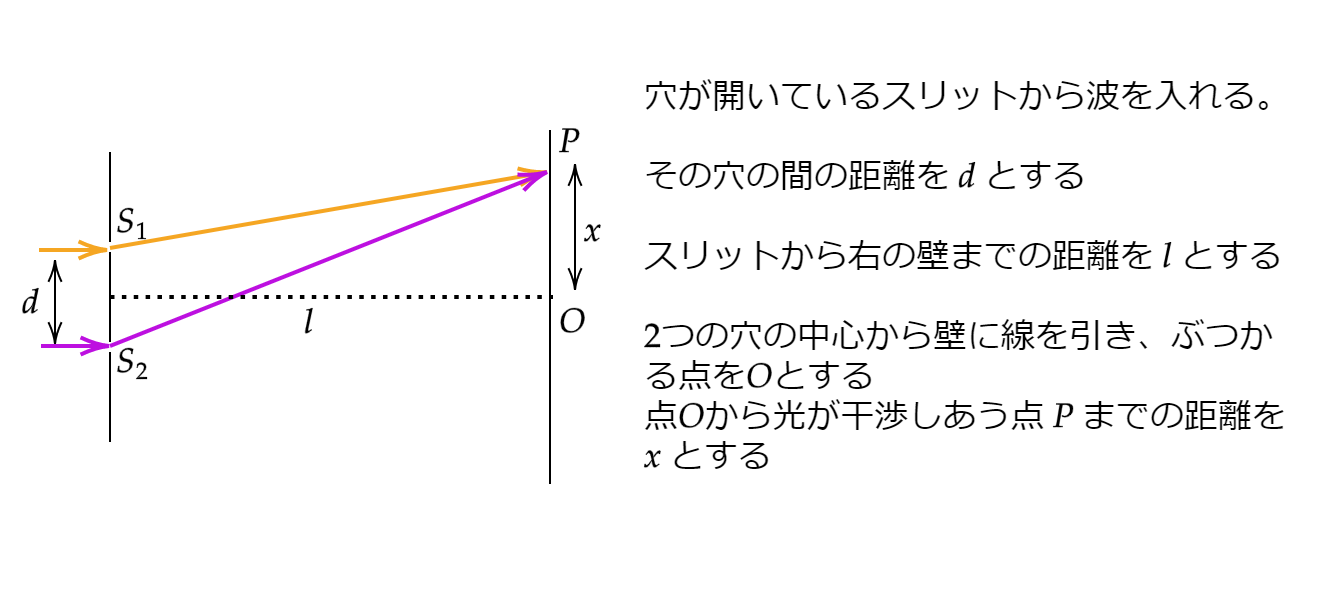
スリット \(S_1\) と \(S_2\) の間隔を \(d\) とし、スリットとスクリーンの距離を \(l\) 、スクリーンの中心 \(O\) からスクリーン上の点Pとの距離を \(x\) とします。
\(S_1,S_2\) から \(P\) までの経路差\(|l_1-l_2|\)は
$$|l_1-l_2|=\sqrt{l^2+(x+\frac{d}{2})^2}-\sqrt{l^2+(x-\frac{d}{2})^2}$$
ここで近似式
$$(1+h)^n \simeq (1+nh)$$
を使いたいので少し変形します。
(今はこの近似は暗記しましょう。突然出てきて戸惑う受験生が多いかと思いますが、高校物理に出てくる近似式は他にほとんどないので安心してください。)
見やすくするため、先ほどの式()のルートを1/2乗になおします。
$$\sqrt{l^2+(x+\frac{d}{2})^2}-\sqrt{l^2+(x-\frac{d}{2})^2}=(l^2+(x+\frac{d}{2})^2)^{\frac{1}{2}}-(l^2+(x-\frac{d}{2})^2)^{\frac{1}{2}}$$
\(l\) を()の外に出したいのでこんなふうに変形します。
$$=(l^2+l^2(\frac{x+\frac{d}{2}}{l})^2)^{\frac{1}{2}}-(l^2+l^2(\frac{x-\frac{d}{2}}{2})^2)^{\frac{1}{2}}$$
\(l\) を外に出します。
$$=l\times (1+(\frac{x+\frac{d}{2}}{l})^2)^{\frac{1}{2}}-l\times (1+(\frac{x-\frac{d}{2}}{2})^2)^{\frac{1}{2}}$$
ここで
$$(\frac{x+\frac{d}{2}}{l})^2=h$$
とします。そうすると
$$=l\times (1+h)^{\frac{1}{2}}-l\times (1+h)^{\frac{1}{2}}$$
これは先ほど紹介した近似式()になっています。\(l\) が付いていてわかりにくいかもしれませんがそれは無視してくださいね。ということで次のように変形できます。
$$=l\times (1+\frac{1}{2}h)-l\times (1+\frac{1}{2}h)$$
めんどうくさいですが \(h\)をもとに戻して計算しましょう。
$$=l\times (1+\frac{1}{2}\times (\frac{x+\frac{d}{2}}{l})^2)-l\times (1+\frac{1}{2}\times (\frac{x-\frac{d}{2}}{l})^2)$$
引き算ですので共通部分はすべて消えます。(わからないひとはすべて展開しよう!)
よって
$$=(\frac{1}{2l}\times 2\cdot x\cdot \frac{d}{2})-(\frac{1}{2l}\times 2\cdot x\cdot -\frac{d}{2})$$
$$=d \frac{x}{l}$$
これで経路差がやっと出ました…
長かったですね。そのため明暗条件は経路差が波長の整数倍(半整数倍)になるので
明線の条件は
$$d \frac{x}{l}=m\lambda$$
暗線の条件は
$$d \frac{x}{l}=(m+\frac{1}{2})\lambda$$
ただし\(m=0,1,2,…\)です。
よって間隔 \(\Delta x\) は
$$(m+1)\lambda – m\lambda =d \frac{x_2}{l} – d \frac{x_1}{l}$$
$$\lambda =d \frac{\Delta x}{l}$$
$$\Delta x =\frac{l\lambda}{d}$$
はい。これが距離差と波長の関係です。
実は簡単にわかる別解があるので載せます。
\(S_1\) と \(S_2\) の中間点を点 \(Q\) としましょう。\(QO\)と \(QP\) のなす角を \(\theta\) とすると
$$\sin\theta \approx \tan\theta =\frac{x}{l}$$
経路差は\(d\sin\theta\)で表せるから
$$d\sin\theta =d\frac{x}{l}$$
となりました。簡単ですね。
入試問題としては?
だいたい2つのパターンが出題されます。
1.誘導付きで隣り合う明線(暗線)の間隔を導く
2.波長の長さを変えると線は上に動くか下に動くか?
のどちらかがよく出ます。
1に関しては特にいうことはありませんね。2は結果の式()に実際に代入してみればわかるかと思います。
まとめ
今回はヤングの実験について学びました。
入試において時々見かけますのでぜひマスターしましょう!
次はこちら3-8回折格子~ニュートンリング