前回はこちら!1-7運動量と力積
ここから円運動です。
力学はもう少しで終わりなので頑張りましょう!
用語集
とりあえず用語を覚えましょう。
| 用語 | 単位 | 説明 |
| 円運動 | 円周上を運動することです。ここでは等速円運動を見ていきます | |
| 角速度 | ラジアン毎秒[rad/s] | 1秒当たりの物体の回転数 |
| 周期 | [s] | 円運動している物体が1周するのに必要な時間 |
| 回転数 | ヘルツ[Hz] | 1秒間に回転する数 |
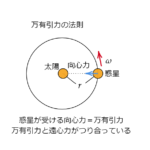
| 向心力 | [N] | 等速運動する物体が円の中心に向かってはたらく力 |
| 慣性力 | [N] | 観測者が加速度運動していることが原因となって表れる見かけ上の力 |
| 遠心力 | [N] | 観測者が物体とともに円運動をするときの慣性力のこと |
○○力という言葉が多くなっています!しっかり区別しましょう!
等速円運動
円周上を等速で動く運動のことを等速円運動といいます。
いままでは直線上や平面上の運動を扱っていましたが、ここから円周上の運動を取り扱います。
今までと大きく変わる点は同じ運動が繰り返されるということです。
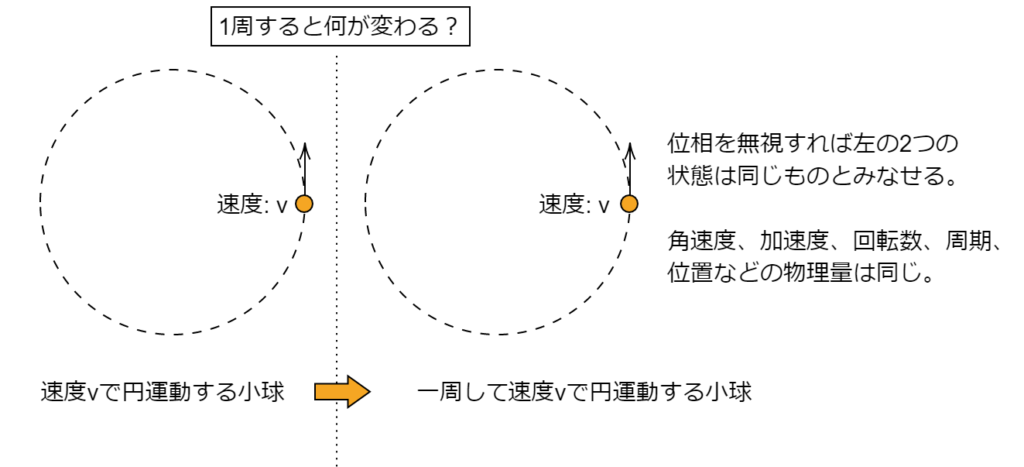
円運動の速度と加速度と向心力
さて、いままでは「速度」という言葉を使っていましたが、この分野では「角速度」という言葉が活躍します。
角速度は小学校、中学校の理科にも出てこなかった物理量だと思いますので定義を忘れないようにしましょう!
角速度はω(オメガ)で表すことが多いです。定義がこちら
$$\omega=\frac{\theta}{t}$$
日本語で表すと(角速度[rad/s]=回転角[rad]/経過時間[t])です。
意味は「1秒あたりに何度回転するか」です。
単位で出てくる[rad]は数学1の三角関数で学んだはずですので忘れた人は復習して思い出しましょう
(\(l=r\theta\) の関係があります。ここで「\(l\)」は円の弧の長さ、「\(r\)」は円の半径)
その角速度を使うと速度・加速度・角速度の関係がこのようになります。
$$a=\frac{v^2}{r}=r\omega^2$$
忘れやすい式ですが是非おぼえてください。
遠心力
観測者が物体とともに円運動をするときの慣性力のことを遠心力といいます。
遠心力の強さは「運動方程式」と「速度・加速度・角速度」関係性より
$$F=ma=mr\omega^2=m\frac{v^2}{r}$$
となります。
遠心力の向きは回転する物体に対して外側に働きます。(”遠”心力だから遠い方向、つまり”外”側と覚えればok!)
問題
ここらで一問解いてみましょう。
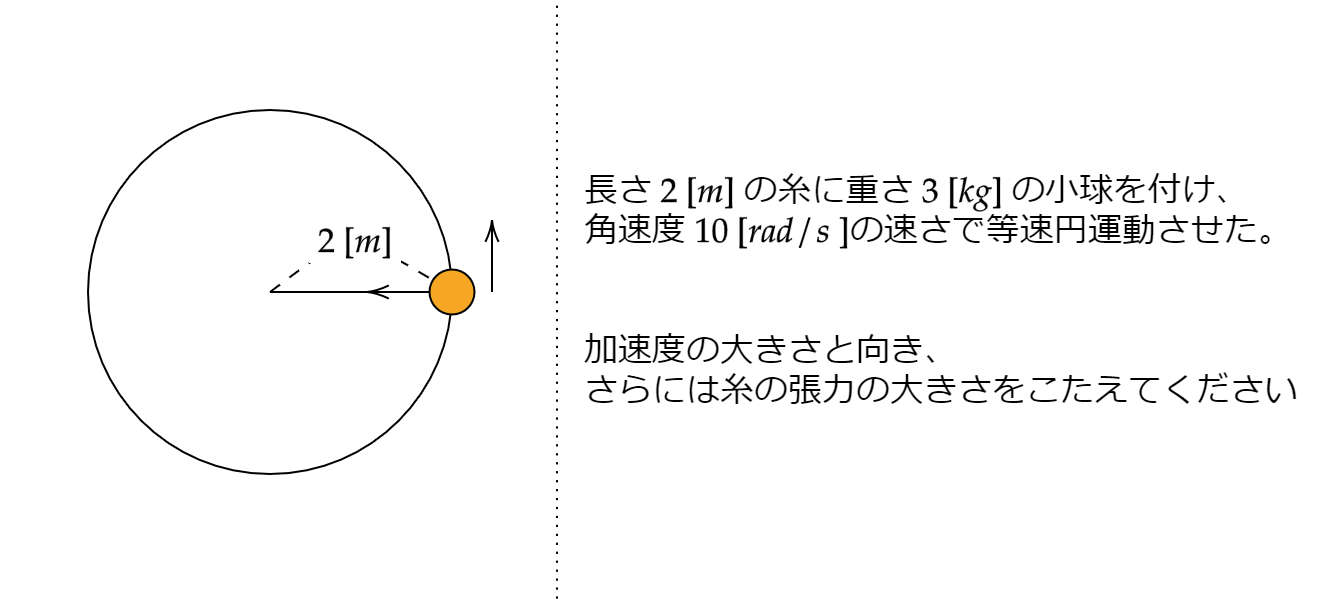
上の図にあるとおり、糸についている小球が等速円運動をしています。
このときの小球の角速度と糸の張力を求めましょう。
では答えを書きます。
加速度と角速度の関係は覚えていますか?
$$a=\frac{v^2}{r}=r\omega^2$$
でしたね。よって
$$a=r\omega^2$$
$$a=2\times 10^2$$
$$a=200$$
となります。向きは \(m\vec{a}=\vec{F}\) より、加速度と力の向きが同じですので、向心力の方向にです。
したがって加速度は円の中心に向かって200 [m/s^2]の大きさ。
糸の張力は運動方程式より
$$3\times 200=F$$
ということで600 [N]です。
(値がやたら大きいような…)
まとめ
今回は等速円運動の基本を学びました。
今まで出てこなかった円周上の運動でのキーポイントはやはり角速度です。この言葉の定義や単位を忘れずに理解することがこの分野の重要な点ですのでしっかりと覚えましょう!
次はこちら!1-9単振動