前回はこちら!1-5運動方程式
ここでは「エネルギー」について学びます。
エネルギーは力学だけではなく他の分野でも出てくる言葉で、非常に重要です。
用語集
○○エネルギーという言葉がたくさん出てきますが、迷わないように覚えましょう!
| 言葉 | 式 | 説明 |
| 仕事 | \(W=Fx\) 単位は[J](ジュール) |
距離\(\times\)その方向に働いた力 |
| 仕事率 | \(P=W/t\) 単位は[W](ワット) |
単位時間あたりにする仕事。仕事の効率の良さを表す |
| 運動エネルギー | \(K=\frac{1}{2}mv^2\) | 速さ \(v\) [m/s]の物体が持つエネルギー |
| 位置エネルギー | \(U=mgh\) | 基準点から高さ \(h\) [m]にある物体が持つエネルギー |
| 弾性エネルギー | \(U=\frac{1}{2}kx^2\) | ばねなどの伸び縮みする物体が蓄えるエネルギー |
| 力学的エネルギーの保存 | \(U_{total}=K_1+U_1=K_2+U_2\) | 物体が保存力だけから仕事を受けるときその和が一定 |
(「単位時間当たり」=「1秒間に」と考えて大丈夫です。)
それではひとつひとつ説明します!
仕事
ここでは仕事の定義が重要です。後ほど3つのエネルギーの話をしますが、3つとも仕事の定義から説明ができます。
物体に大きさF[N]の力を加え、その方向に移動させたときに、仕事をしたといいます。仕事をW[J]で表すと
$$W[J]=\vec{F}[N]\cdot \vec{x}[m]$$
となります。日本語で書くと「仕事=力×移動距離」です。なお、単位は[J]ジュールです。
また出てきました。ベクトルの内積です。cosθの登場です。
「力の向き」と「進んだ距離の方向」が同じ向きであれ cosθ は1になります。しかし、 θ が90°のときは cosθ がゼロになるので仕事はゼロになることに注意!
( θ が90°のときは2つ根ベクトルが垂直な関係にありますよね。)
仕事率
仕事率とは単位時間あたりにする仕事を意味しており、仕事の効率の良さを表しています。この値が大きければ1秒間にするたくさんの仕事をするという意味になります。
$$P=W/t$$
(「単位時間当たりする仕事」とは「1秒間にする仕事」という意味です。)
この仕事率 \(P\) の単位は[W]で表し、「ワット」と読みます。
(仕事のWとは違うので注意です…)
運動エネルギー
さて、エネルギーには様々な種類があります。
例えば、ばねが伸び縮みした時に蓄えられる「弾性エネルギー」や、コンデンサーに電圧をかけた時に蓄えられる「静電エネルギー」などなど。
物理のあらゆる分野で出てくるエネルギーの中でも、今回は運動エネルギーについて説明します。
式はこんな感じです。
$$K=\frac{1}{2}mv^2$$
英語で運動を意味する「kinetic」の頭文字をとってKとしました。
\(m\) はいつも通り質量[kg]で、\(v\) は速さ[m/s]を意味します。
ここで \(m\) は物質によって決まるので定数とみなすと、運動エネルギーは速さの二乗に依存する物理量だといえます。
つまり注目している物体が速く動いていれば運動エネルギーは大きいし、ゆっくり動いていれば運動エネルギーは小さいということになります。
もちろん物体が動いていないときは速さがゼロつまり \(v=0\) ですので運動エネルギーもゼロになります。
一応導出してみましょうか。
速さ \(v\) [m/s]で移動している、質量 \(m\) [kg]の車が \(x\) [m] 進んだところで止まったとします。
そしてこの車を大きさ \(F\) [N]の力で、手で止めたとします。このとき作用反作用の法則から車に大きさ \(F\) の力がかかったことになります。
運動方程式は
$$ma=-F$$
となります。また、車は等加速度運動したのでこちらの式
$$v_x^2-v_0^2=2ax $$
$$ 0-v^2=2ax$$
が成り立ちます。この二つの式を代入すると
$$Fx=\frac{1}{2}mv^2 $$
$$K= \frac{1}{2}mv^2 $$
となります。できましたでしょうか?(エネルギー=仕事=力\(\times\)距離)
重力による位置エネルギー
重力 \(g\) [m/s^2]によって引き起こされる位置 \(h\) [m]に関するエネルギーを重力による位置エネルギーとよび
$$U=mgh$$
で表します。また、一般的に「重力による」は言わなくても伝わるケースが多いので省略して、「位置エネルギー」と呼ばれることが多いです。
式に出てくる \(h\) [m]は高さを表す「height」の略です。
簡単に導出をします。
仕事(エネルギー)は簡単に「仕事=力×距離」で表せます。
運動方程式を見直せば思い出せるのですが「質量×加速度=力」になりますよね。つまり「\(mg\)」は力を表しています。(ただし \(g\) は重力加速度)
そして \(h\) [m]は基準点からの距離を表しているので
「\(mg\)(力)× \(h\)(距離)=エネルギー」になります。

基準点は自分で考えるのでどこにとっても良いです。
ただ、上の図でいうと地面を基準にすると式が2つ出てきてしまうのに対し、小球1の高さを基準にすると小球1のエネルギーはゼロになり、式が一つで済みます。
位置エネルギーの基準は式の数が少なくなるように取りましょう!
弾性力による位置エネルギー
伸び縮みしたばねなどが蓄えるエネルギーを弾性力による位置エネルギーと呼びます。ただ長いので「弾性エネルギー」と呼ばれることが多いです。
$$U=\frac{1}{2}kx^2$$
ここで \(k\) [N/m]はばね定数、\(x\) [m]は自然長の長さからの変位を表しています。
ばね定数とは物質に固有の定数で、どのくらいばねがの縮みするのかをあらわします。
入試では問題文にばねがあればこの弾性エネルギーの式を使う可能性が非常に高いです。
反対に問題文にばねが登場しなかったら弾性エネルギーの式を使わないケースが多いです。
力学的エネルギー保存則
この保存則は入試問題を解くうえでものすごーく使います。
「物体が保存力だけから仕事をされるとき、その和は一定に保たれる」というものです。ここでいう保存力は「運動エネルギー」「位置エネルギー」「弾性エネルギー」のことを指します。
$$E_{total}=K_A+U_A=K_B+U_B$$
(Kは運動エネルギー、Uは位置エネルギー、AとBはある地点)
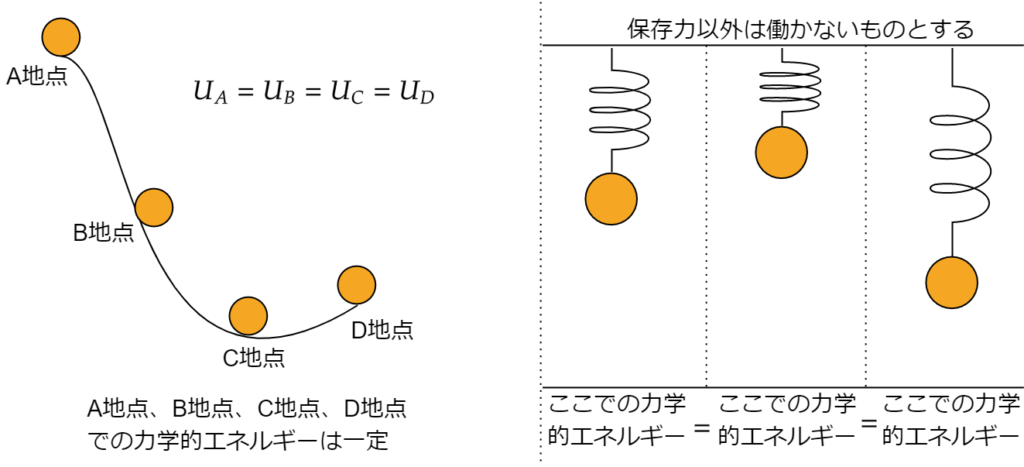
空気抵抗や摩擦を考えないとき上の左図のように小球の持つ力学的エネルギーがどの地点においても一定になります。
これを利用し、方程式を立てて問題を解くというケースが多いです!
まとめ
今回はエネルギーについて学びました。
エネルギーはどの分野でも出てくる非常に重要な概念です。
是非マスターしましょう!
次はこちら!1-7運動量と力積