前回はこちら1-4力のつり合いと作用反作用
力学で最重要といっても過言ではないと思います。
様々な問題に出てきます。本当によく見かけます。
運動の3法則
ニュートンの運動の法則はこちらです。
- 慣性の法則
- 運動の法則・運動方程式
- 作用反作用
以下ではそれぞれを簡単に説明します。
慣性の法則
慣性の法則とは
「物体が外力を受けない、もしくは外力が釣り合っている限り、静止している物体は静止し続け、運動している物体は等速度運動しつづける」
というものです。
物体は今している運動をし続けようとする性質を慣性と呼びます。
運動の法則・運動方程式
運動方程式はこちらです。
$$m\vec{a}=\vec{F}$$
これは後程説明します。
作用反作用
こちらは前回説明しました。
2つの物体間で及ぼしあう力で、一方を作用と呼ぶとき、もう一方を反作用と呼びます。
この作用反作用は重力や電磁気力などの遠隔力にも働きます。すごいですね。
運動方程式 \(m\vec{a}=\vec{F}\)
\(m\) は質力[kg]、\(a\) は加速度[m/s^2]、\(F\) は力[N]です。
加速度がゼロの場合を考えてみましょう。
加速度がゼロとは
- 物体が静止している
- 物体が等速度運動している。
のどちらかであると考えられます。
注意してほしいのは等速度運動しているときも加速度がゼロになるということです。
そして加速がゼロのとき、右辺の力 \(F\) も当然ゼロになります。
右辺がゼロということは
- 加速度と同じ方向にその物体に力が働いていない
- 力がつり合っている
のどちらかが考えられます。
力と加速度の向きを確認しましょう
運動方程式を見直してください。力の向きは加速度の向きと同じです。
運動方程式の使い方
運動方程式の使い方を簡単な例題で確認してみましょう。
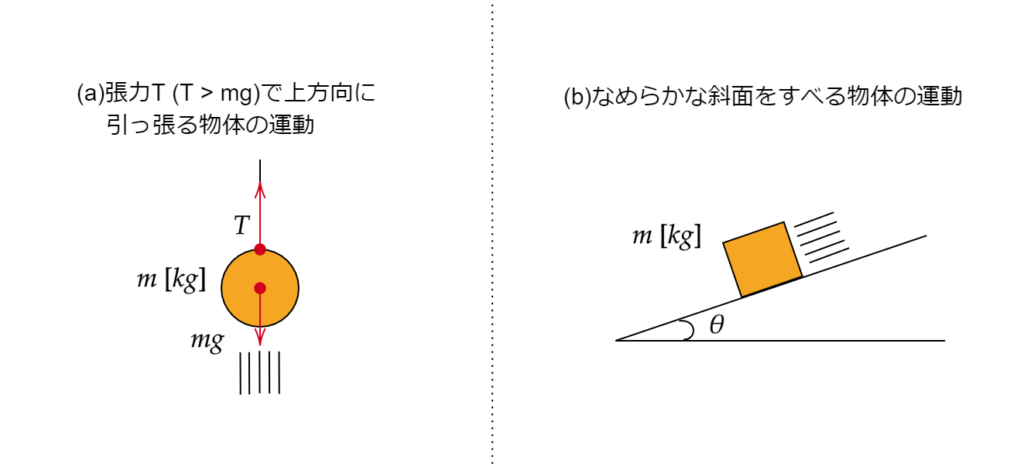
運動方程式の立て方を5ステップに分けて説明したいと思います。
その5ステップは以下の通りです。
- 問題文を読み、図を描く
- 物体が受ける力をすべて図に書く
- 正の向き(運動している向きを正とすることが多い)を決める
- 鉛直方向と水平方向に分ける
- 運動方程式に代入する
とりあえず左側の\(a\)の問題を例に解いてみましょう。
~問題\(a\)の解き方~
ステップ1,2はすでに終わらせておきました。
ステップ3:鉛直上向きを正とします。なお、この問題ではステップ4は不要です。
ステップ5:運動方程式に代入する
$$ma=T-mg$$
こんな感じですね。これで運動方程式は完成です。
次に問題\(b\)を解いてみます。こちらはすこしわかりにくいですね。力を図に書いてみましょう
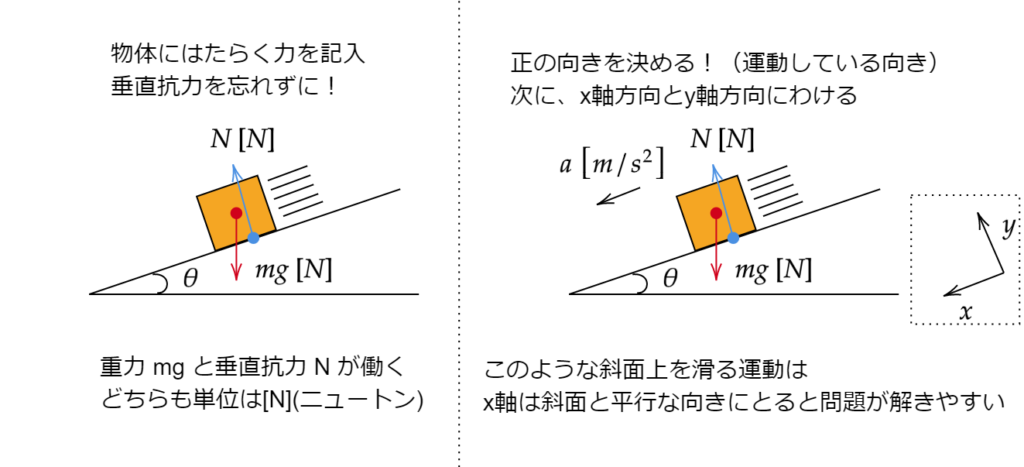
物体に働く力を図に書きましょう。これができないと先へ進めません。
次に正の向きを決めます。これはたいてい物体が運動している方向にすることが多いです。
そしてx軸とy軸を決めます。物体が斜面を滑る問題ではx軸を斜面と平行にとると問題が解きやすくなります。
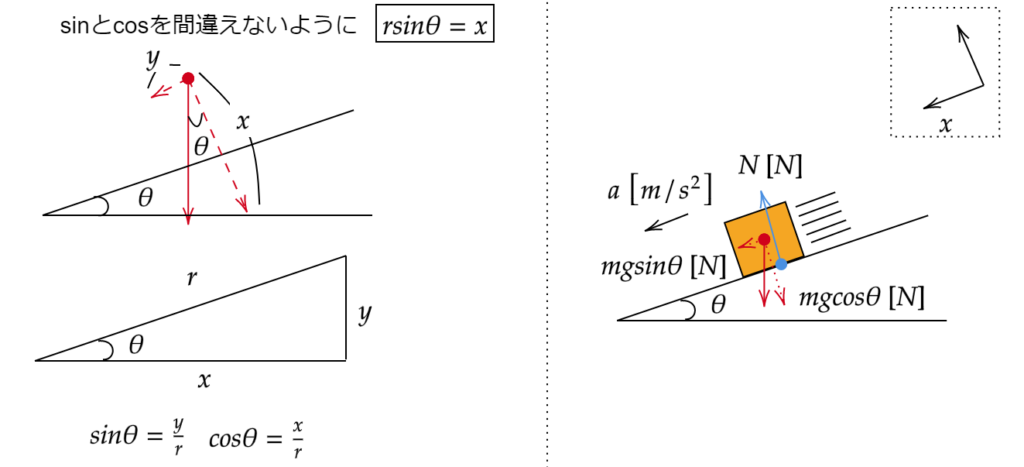
斜面問題でよく間違えるのがθの位置です。それを間違えるとsinと\cosを逆に書いてしまうでしょう。図を見て確認してください。
それができれば式を立てられます。x軸方向は
$$ma=mg sin\theta$$
y軸方向は上方向を正として
$$ma=N-mg \cos\theta$$
となります。なお、物体はy軸方向に動いていないのでこれは釣り合っています。
$$N=mg \cos\theta$$
こうなります。以上です。
まとめ
今回は運動方程式を学びました。
力学で重要な分野ですのでしっかり身につけましょう!
次はエネルギーについて学びます!
1-6エネルギーはこちら!