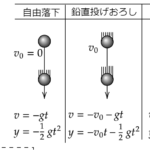
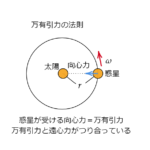
前回はこちら!1-2落下・投げ上げ・放物運動
ここでは「剛体」「モーメント」について説明します。
前回の放物運動は小球(大きさを無視した物体)を取り扱いましたが、今回は違います。
大きさを考える剛体を使います。
用語説明
まずはこのページで重要な用語を簡単に説明します。
| 名前 | 説明 |
| 質点(しつてん) | 大きさを無視できる物体 |
| モーメント | 物体の回転させる力の大きさのこと モーメントが大きいとは物体が回転しにくいということ |
| 剛体(ごうたい) | 力を加えても変形しない理想的な物体 |
| 偶力(ぐうりょく) | 同じ大きさで反平行(向きが逆向きで平行)な2つの力 |
| 重心(じゅうしん) | 重力の作用点 |
計算だけでなく用語を覚えることも重要です!
力のモーメント
大きさを無視できる質点では、力のベクトルだけを考えればよいのですが、大きさがある物体では、物体に力を加えると縦や横に動くだけではなく、回転をすることがあります。
ここでは回転する物体の運動を数式で表してみます。
$$M=Fl \sin\theta$$
(\(M\) を力のモーメントと呼びます。基準点から作用点への距離ベクトル \(l\) [m]と力の向き \(F\) [N]が直角であれば \(\sin\theta\) は1になります。)
さて、この力のモーメント \(M\) [N\(\cdot\)m]は、回転させる力のはたらきを表しています。単位は「ニュートンメートル」です。
モーメントが大きいということは「たくさん力を加えなければその物体は回転してくれない」ということです。
回転しやすいではないですからね、気を付けてください。回転のしにくさを表す物理量です。
なお、力のモーメントを考える問題では基準点が大事です。
基準点は自分で決められます。そのため、どこを基準にすればよいかを考えて問題を解きましょう!
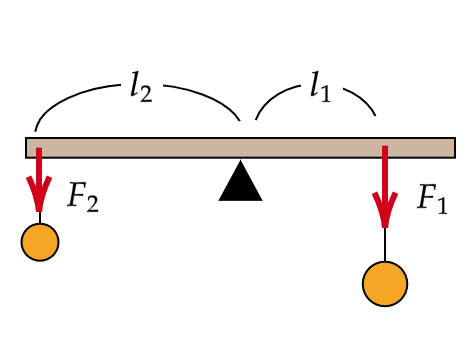
剛体のつり合いと合成
剛体のつり合い
ここから剛体について考えていきます。
力を加えても変形しない理想的な物体を剛体といいます。
剛体がつり合うための条件は2つあります。(つりあうとは平行運動も回転運動もしない状態、つまり静止していることです。)
- 剛体に働いている力のベクトル和がゼロ
- 剛体に働くモーメント和がゼロ
これを数式で表すと以下のようになります。(モーメントをベクトル表記していますがここでは無視しても結構です。)
$$\vec{F_1}+\vec{F_2}+\vec{F_3}+\cdots+ \vec{F_n}=0 $$
$$\vec{M_1}+\vec{M_2}+\vec{M_3}+\cdots+\vec{M_n}=0 $$
これらがつり合いの条件です。
物理全般的に言えることですが「日本語で書かれた用語や条件」と「数式」を結びつけることは非常に重要です。
ここでは「剛体のつり合いの条件」とこちらの数式「 \(\vec{F_1}+\cdots=0\)、 \(\vec{M_1}+\cdots=0\)」が頭の中でしっかり一致させられるように覚えましょう!
剛体の合成
剛体上の点A、Bに平行で同じ向きに力が働くとき、その合力 \(\vec{F}\) は点A、Bに働く力の合計になります。また、その力の作用点Oの位置は点ABを \(\vec{F_2}:\vec{F_1}\) に内分する点になります。
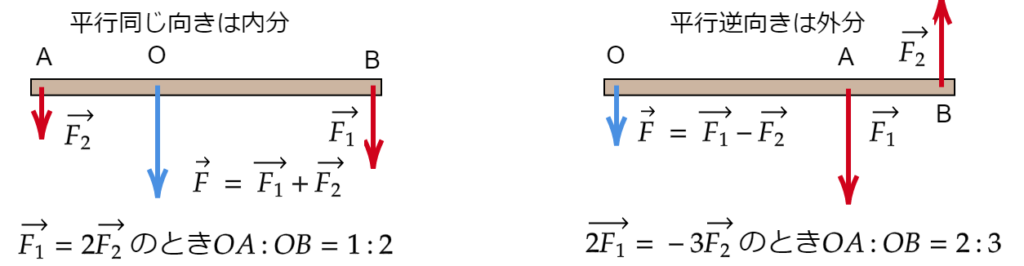
一方、並行で逆向きの力が一つの剛体上に働いている場合、内分ではなく、外分になります。
ここでは「内分・外分」と「ベクトルの合成」という2つの数学の知識が必要になります。
この先も 「内分・外分」と「ベクトル」の知識は多少必要なので、不安な人はまず先に数学を勉強しましょう!
重心
物体には重力が働きます。
剛体を無数の小さな物体の集合体であると考えると、各部分に働く重力の合計の作用点を重心と呼びます。
少しわかりにくいのでいいかえますと、支えれば回転せずに釣り合う点を重心と呼びます。
2つの物体の重心を求める際に使われる式はこちらです。\(x_G\) は重心のx座標で、 \(m\) は質量です。y座標についても同様の式で求められます。
$$x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}$$
物体が3つになれば同じように増やせばOKです。
$$x_G=\frac{m_1x_1+m_2x_2+m_3x_3}{m_1+m_2+m_3}$$
物体の数がn個のときも同様に増やしてください。
重心問題を考えるうえで重要なのはいくつかの図形に分けて考えることです。
問題
2つほど問題を用意しました
是非解いてみましょう!
問題1
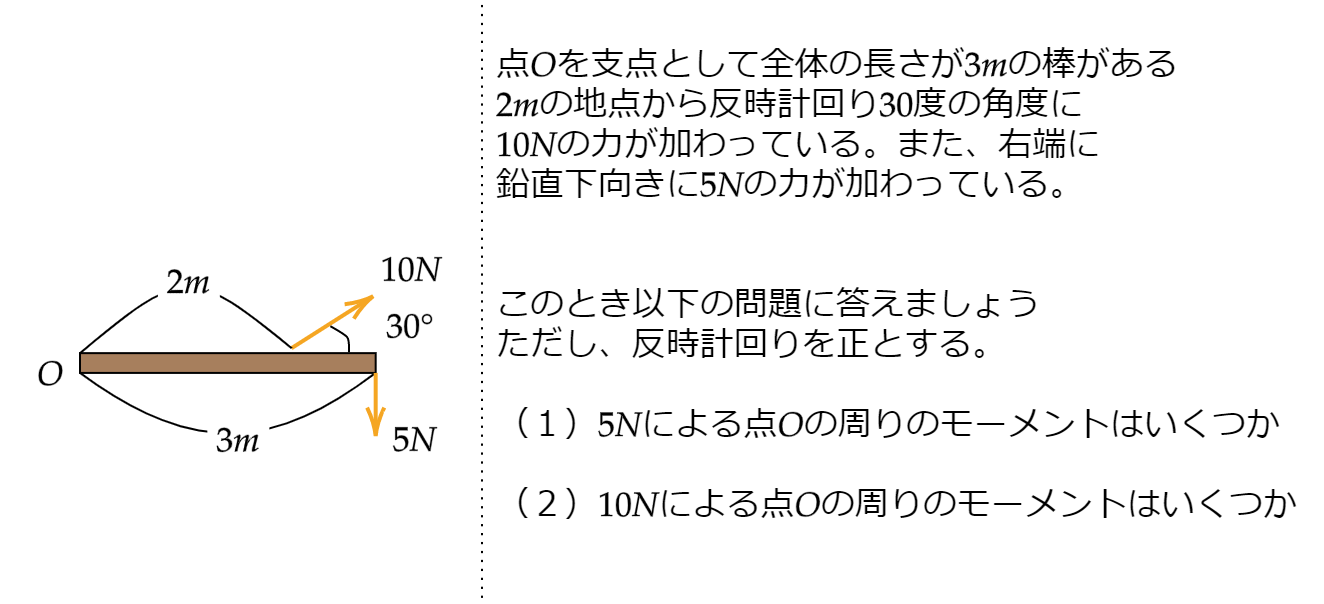
モーメントに関する問題です。
(1)5Nによる点Oの周りのモーメントはいくつか。の答え
点Oを基準として
$$M=-5\times 3$$
$$M=-15$$
反時計回りを正としていますのでマイナスが付きます。
単位はN・mです。
(2)10Nによる点Oの周りのモーメントはいくつか。の答え
点Oを基準として
$$M=10\times 2\times \sin30$$
$$M=10$$
単位はもちろんN・mです。
では次の問題に行ってみましょう。
問題2
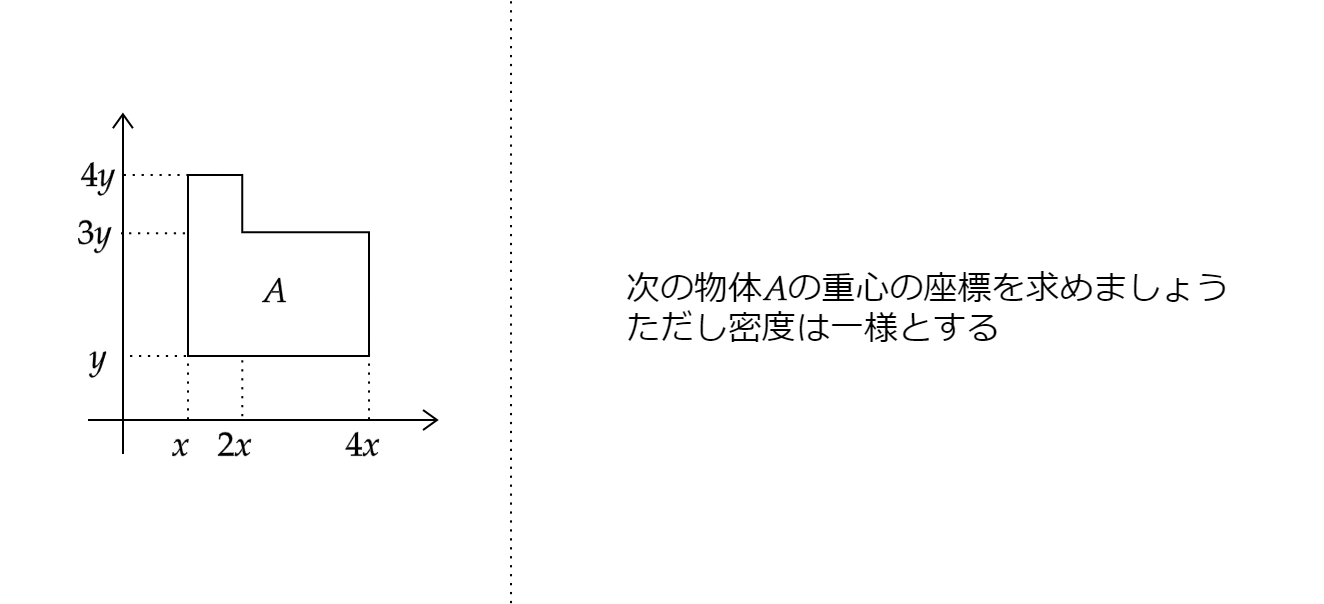
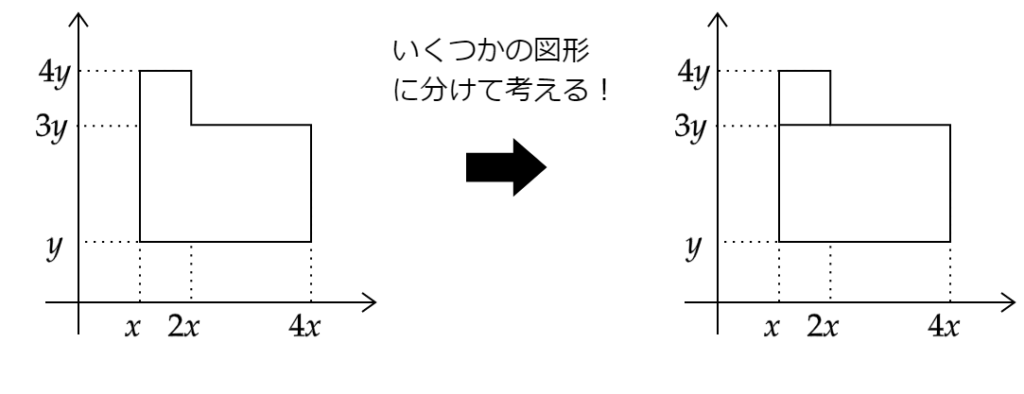
上の図形の重心のx座標を求めてみましょう。
左の図のままでは重心を求めることが難しいです。
そのようなときは右の図のように分けて考えましょう!重心の問題で複雑な図形が出た時は図形をわかりやすく分けて考えることが重要です! よって
$$x_G=\frac{m_1x_1+m_2x_2}{m_1+m_2}$$
$$x_G=\frac{m\times1.5x+6m\times2.5x}{m+6m}$$
$$x_G=\frac{33}{14}x$$
これで結果が得られました!
これであっているか確認してみましょう。\(\frac{33}{14}\)は約2.2 とかでしょうか、まあだいたいあっているでしょう。
適当でよいので結果が出たら確認してみてください! もし、結果があり得ないほど大きい値や、マイナスなどになっていたら確実に計算ミスをしたと気づけるからです。
y座標についても同様です。
$$y_G=\frac{m_1y_1+m_2y_2}{m_1+m_2}$$
$$y_G=\frac{m\times3.5y+6m\times2y}{m+6m}$$
$$y_G=\frac{31}{14}x$$
となります。
よって重心の座標は
$$(x,y)=(\frac{33}{14}x,\frac{31}{14}y)$$
となります。これが答えです。
まとめ
今回は剛体と力のモーメント、それに重心について取り扱いました。
これらは学ぶべき内容は少ないのですが、問題は作りやすいです。
インプットだけでなく、実際に問題を自分で解いてみてください!
次はこちら!1-4力のつり合いと作用反作用