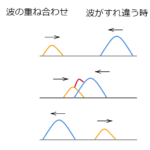
今回は高校波動分野に出てくる公式と用語を載せました。
復習用に使ってください!
公式集
ではいきます。
| 用語・名前 | 公式 | 説明 |
| 振動数と周期 | $$f=\frac{1}{T}$$ | 振動数 \(f\) は1秒間の振動の回数を表したものです。
周期は \(T\) は媒質が1回の振動に要する時間のことです。 |
| 波の速さ | $$v=\frac{\lambda}{T}=f\lambda$$ | \(\lambda\) は波長です。
波長とは隣り合う山と山の間隔のことです。 |
| 正弦波の式 | $$y=A\sin\frac{2\pi}{T}(t-\frac{x}{v})$$ | \(A\) は振幅です。
|
| 干渉(強め合い) | $$|l_1-l_2|=m\lambda $$ | ただし同位相のとき。ちなみに \(m=0,1,2,…\)です。
逆位相の場合は m が \((m+\frac{1}{2})\) になります。 2つの波が強め合うための条件。距離の差が波長の整数倍 |
| 反射の法則 | $$\theta =\theta’$$ | 入射角 \(\theta \) と反射角 \(\theta’ \) が等しいという法則 |
| 屈折の法則 | $$\frac{\sin\theta_1}{\sin\theta_2}=\frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2}=n_{12}$$ | 入射角と反射角、それに媒質1での速さや波長と媒質2での速さや波長との関係 |
| 光の全反射 | $$\sin\theta_C=\frac{1}{n}$$ | 入射光がすべて反射してしまう現象のこと。
\(n\) は媒質の屈折率 |
| 音速 | $$V=331.5+0.6t$$ | 空気中の音の速さ。\(t\) は温度 |
| うなりの振動数 | $$f=|f_1-f_2|$$ | うなりとは(言葉で表現しづらいのですが)「うぉーん うぉーん」と聞こえる現象のこと。2つの差の絶対値を取るだけ。 |
| 弦を伝わる波の速さ | $$v=\sqrt{\frac{S}{\rho}}$$ | 弦の張力は \(S\) 、線密度は \(\rho\) |
| 弦を伝わる波の振動数 | $$f_m=\frac{m}{2l}\sqrt{\frac{S}{\rho}}$$ | ただし\((m=1,2,3,…)\)「振動数×波長=速さ」ですのでこのようになりました |
| 閉管の振動 | $$l=\frac{\lambda}{4}(2m-1)$$ | \(l\) は管の長さ。mは整数。 |
| 開管の振動 | $$l=\frac{\lambda}2m$$ | 上と同様 |
| ドップラー効果 | $$f’=\frac{V-v_0}{V-v_s}f$$ | 音源 \(v_s\) が近づき、観測者 \(v_s\) が遠ざかる場合の振動数。 |
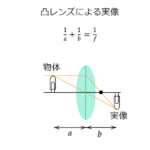
| 凸レンズによる実像 | $$\frac{1}{a}+\frac{1}{b}=\frac{1}{f}$$ | \(a\) がレンズから物体までの距離
\(b\) がレンズから像までの距離 \(f\) は焦点距離 |
| 凸レンズによる虚像 | $$\frac{1}{a}-\frac{1}{b}=\frac{1}{f}$$ | 虚像の場合は \(b\) にマイナスが付く |
| 凹レンズによる実像 | $$\frac{1}{a}+\frac{1}{b}=-\frac{1}{f}$$ | 凹レンズのの場合は \(f\) にマイナスが付く |
| レンズの倍率 | $$m=\frac{a}{b}$$ | 倍率です。レンズの。はい。 |
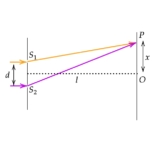
| \(|h|<<1\)のときに成り立つ近似式 | $$(1+h)^n \simeq (1+nh)$$ | 近似式はいろいろとありますが、高校物理出てくるのは数少ないです。ヤングの実験に出てきます。 |
| ヤングの実験に出てくる明線の間隔 | $$\Delta x =\frac{l\lambda}{d}$$ | 公式ではないです。計算すれば出てきますが、有名ですので覚えておきましょう。 |
| 格子定数を \(d\) 、光の波長を \(λ\) とした時の光が強め合う条件 | $$d\sin\theta = m\lambda$$ | 2つの光の経路差が波長の整数倍のとき強め合います。 |
| 薄膜による干渉の明線条件 | $$2nd\cos\theta=(m+\frac{1}{2})\lambda$$ | 1回位相が \(\pi\) 反転しているため、
2つの光の経路差が波長の半整数倍のとき強め合います。 |
| くさび型空気層における干渉の明線条件 | $$2d=2x\frac{l}{L}=m\lambda$$ | 2つの光の経路差が波長の整数倍のとき強め合います。
半整数倍のとき弱めあいます。 |
| ニュートンリングの明環の半径 | $$r=\sqrt{(m+\frac{1}{2})\lambda R}$$ | 計算すれば出てきますが覚えておいて損はないと思います。。 |
いかがでしょうか?
思ったより少ないのではないでしょうか?
次は用語を覚えましょう!
用語集
ではいきます。
| 用語 | 説明 |
| 波 | 振動が次々と周りに伝わる現象 |
| 媒質 | 波を伝える物質 |
| 波源 | 振動の発生源 |
| 波形 | ある瞬間における波の形 |
| 振幅 | 波の高さのこと |
| (波形の)山・谷 | 波形の最も高いところを山、最も低いところを谷 |
| 波長 | 波形の山と山の間隔 |
| 位相 | 振動状態を表す量のこと |
| 縦波 | 波の進行に動く波のこと |
| 平面波 | 波面が直線または平面である波のこと |
| 球面波 | 波面が球面または円である波のこと |
| 干渉 | 複数の波が重なり、強め合ったり弱めあったりすること |
| 反射の法則 | 壁に平面波が入るとき、入射角と反射角が等しくなること |
| 射線 | 波の進む向きを示す矢印のこと |
| 屈折角 | ある境界面に波が入るとき、境界面と法線部と波の進む向きとのなす角 |
| 屈折の法則 | 入射角・反射角と波の速度や波長、屈折率との関係式 |
| 回折 | 波が障害物の背後に回り込む現象のこと |
| 波の独立性 | 2つ以上の重なった波がその後、お互いの影響を受けずにそのまま進むこと |
| 節・腹 | 定常波において常に振動しない部分を節、振幅が最大になる場所を腹という |
| 自由端反射 | 入射波が壁に当たったとき位相の反転がなくそのまま反射すること |
| 固定端反射 | 位相の反転があり、入射波を打ち消すような反射 |
| ホイヘンスの原理 | 球面波は波の進む速さと等しい速さで広がり、これら無数の球面波に共通する面が次の瞬間の波面になる現象のこと |
| (相対)屈折率 \((n_{12})\) | \(n_{12}\) は媒質1と媒質2によって決まる一定の値、大きければ屈折角が大きくなる |
| 音 | 狭義的には空気中に伝播する波のこと |
| うなり | 振動数のわずかに異なる音を2つ同時に鳴らした時に起きる現象のこと |
| 固有振動数 \(f\) | 物体が持っている振動数で、一番振動しやすい値のこと |
| 共振・共鳴 | 振動する物体が外部の振動に反応して大きく振動すること |
| ドップラー効果 | 観測者と波の発生源の相対的な速度の存在によって聞こえてくる音と物体の振動数が異なって聞こえる現象のこと |
| 光速 \(c\) | 光の速さ。その値は\(c=2.99792458\times 10^8\)m/s |
| 光の反射 | 光が屈折率の違う媒質に入射するとき一部が跳ね返ること |
| 全反射 | 光が屈折率の違う媒質に入らず、すべて反射してしまうこと |
| 分散 | 光が波長ごとに分裂すること |
| スペクトル | 光の帯のようなもの |
| 可視光線 | 人間の目に見える光のこと。その波長の範囲はおおよそ380nm~780nm |
| 散乱 | 光が粒子にぶつかって曲がること |
| 偏光 | 振動が一方向だけの光のこと |
| 臨界角 | 全反射するときの入射角のこと |
| 凹レンズ(おうれんず) | 漢字のようにへこんでいるレンズのこと |
| 凸レンズ(とつれんず) | 漢字のように膨らんでいるレンズのこと |
| 焦点 | レンズに光を通した時に通過した光が集まる点のこと |
| 焦点距離 \(F\) | レンズの中心から焦点までの距離 |
| 実像 | レンズを通過した光が実際に集まってできる像 |
| 虚像 | 実際に物体があるように見える像 |
| 回折格子 | カラス板などの一面に平行で等間隔の数千本ものすじを引いたもの |
| 格子定数 \(d\) | 隣り合うスリットに間隔。単位はメートル |
| 薄膜 | 薄い膜のこと |
| 光学距離 | 光が屈折率nの媒質中で進む距離をlとしたとき、真空中で進むnlを光学距離といいます |
| 光路差 | 経路差を光学距離で表したもの |
まとめ
一覧表を作っておいていうのもあれですが、公式は覚えるだけではだめです。
しっかり使えるようにしましょう!