今回は回折格子~波動分野の最後までを扱います。
難しく感じますがやっていることはずっと同じです。
しっかりとマスターしましょう!
用語集
| 用語 | 説明 |
| 回折格子 | カラス板などの一面に平行で等間隔の数千本ものすじを引いたもの |
| 格子定数 | 隣り合うスリットに間隔のこと。単位はメートル |
| 薄膜 | 薄い膜のこと |
| 光学距離 | 光が屈折率 n の媒質中で進む距離を l としたとき、真空中で進む距離 nl のこと。 |
| 光路差 | 経路差を光学距離で表したもの |
では早速行きましょう!
ここで重要なものは?
ここで重要なのは経路差を考えることです。
経路差とはその名の通り2つの(光の)経路の差を表します。
(途中で反射がなければ)光路差が波長の整数倍になるとき、波が干渉して強めあいます。
逆に波長の半整数倍になるとき弱めあいます。
以下で話す内容はすべてこれを考えます!
それでは参りましょう!
回折格子
上で説明したとおり回折格子はガラス板などに数千~数万本の線を引いたものです。
となりあうスリットの間隔を格子定数といいます。
格子定数を d 、光の波長を λ とすると光が強め合う条件(明線条件いいます)は
$$d\sin\theta = m\lambda$$
で表されます。これの左辺は二つの光の経路差を表しています。一方右辺は波長の整数倍は整数mを使って表しています。(ただし m=0.1.2.…)

上図の右側は次の薄膜による干渉です。
薄膜による干渉
次は薄膜による干渉条件を見てみましょう。
薄膜とはその名の通り薄い膜でシャボン玉などが例として挙げられます。
反射光が強め合う条件がややわかりにくいです。
しかし考えていることは今までと同じで、「光の経路差=波長の整数倍」を考えます。
そのとき「屈折率が小さい媒質」から「屈折率がより大きい媒質」へ光が侵入するとき位相が反転し、干渉条件が波長の整数倍ではなく、波長の半整数倍になります。
以下の図で干渉条件を考えると
明線条件は
$$2nd\cos\theta=(m+\frac{1}{2})\lambda$$
になります。
ポイントは \(\cos\theta\) です。どこが直角なのかを考えてみてください。
これと全く同じ形で出題される場合もありますが少し変えて出される場合もありますので経路差を自分で考えて自力で出せるようにしましょう!

くさび形空気層
くさび型の問題も経路差を考えるだけです。
図は以下のようになっています。
明線条件は下のガラスで位相が反転するので
$$2d=2x\frac{l}{L}=(m+\frac{1}{2})\lambda$$
途中で出てきた l/L は \(tan\theta \) に当たります。
明線条件はもちろん
$$2d=2x\frac{l}{L}=m\lambda$$
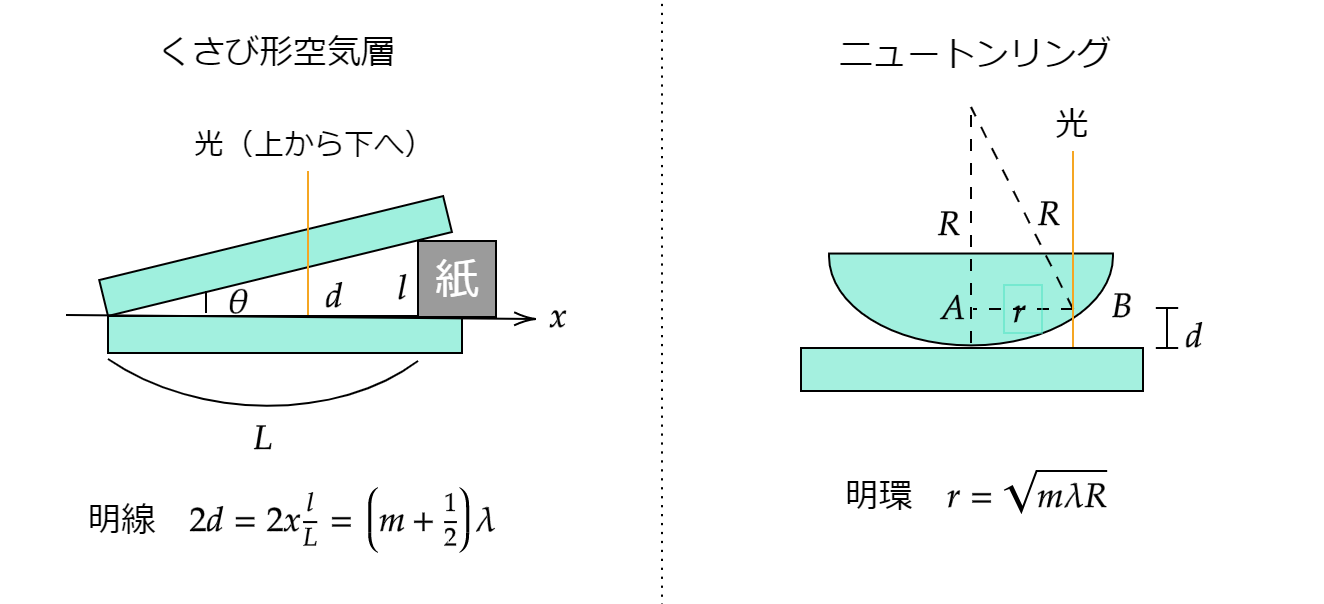
ニュートンリング
ガラスとレンズの接点を中心として上から光を入射すると同心円状に縞模様が観測される現象が起こります。このときできる縞をニュートンリングといいます。
この時の明環条件は
$$r=\sqrt{(m+\frac{1}{2})\lambda R}$$
のようになります。一応導出しましょう。
導出方法
$$d=R-\sqrt{R^2-r^2}$$
$$=R-\sqrt{R^2(1-\frac{r^2}{R^2})}$$
$$=R-R\sqrt{1-\frac{r^2}{R^2}}$$
$$=R-R(1-\frac{r^2}{R^2})^\frac{1}{2}$$
ここで \(|h|<<1\) の時に成り立つ近似式
$$(1+h)^n \approx 1+nh$$
を利用します。いまの状況を当てはめると n=2、h=1/2 にです。よって
$$ \approx R-R(1-\frac{r^2}{2R^2})$$
$$=R-R+\frac{r^2}{2R}$$
$$=\frac{r^2}{2R}$$
これは「d=」の式でしたので
$$2Rd=r^2$$
平らなガラスの方で位相が \(\pi\) ズレるので暗環条件は経路差=波長の整数倍より
$$2d=m\lambda$$
式()より暗環条件は
$$r=\sqrt{m\lambda R}$$
同様に明環条件は
$$r=\sqrt{(m+\frac{1}{2})\lambda R}$$
以上で導けました。
まとめ
今回は波動の最後の分野を説明しました。
力学、電磁気学を優先して曖昧になりやすい分野ですので、しっかりと復習をしてマスターしましょう!
次回はこちら!4-1導体・オームの法則