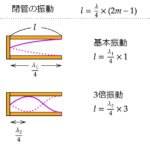
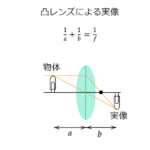
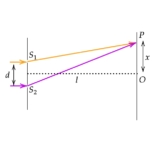
前回はこちら!3-1波の性質
ここでは波の干渉や平面波の屈折について学びます。
干渉とは複数の波が強め合ったり弱めあったりする現象のことを言いまして、波動分野の最後では干渉条件をメインに扱うので非常に重要な用語です。
用語集
| 用語 | 説明 | 用語 | 説明 |
| 平面波 | 波面が直線または平面である波のこと | 球面波 | 波面が球面または円である波のこと |
| 干渉 | 複数の波が重なり、強め合ったり弱めあったりすること | 反射の法則 | 壁に平面波が入るときの入射角と反射角が等しくなること |
| 射線 | 波の進む向きを示す矢印のこと | 屈折角 | ある境界面に波が入るとき、境界面と法線部と波の進む向きとのなす角 |
| 屈折の法則 | 入射角・反射角と波の速度や波長、屈折率との関係 | 回折 | 波が障害物の背後に回り込む現象のこと |
特に干渉と回折は重要です。
これらは波の性質を表しているので、なんらかの実験して干渉や回折の現象がおきれば、その正体が波であると説明できます。
重ね合わせの原理
波Aの位置を \(y_A\) 、波Bの位置を \(y_A\) としたとき、合成波の位置 \(y\) は次のように表されます。
$$y=y_A+y_B$$
です。図で確認しましょう。
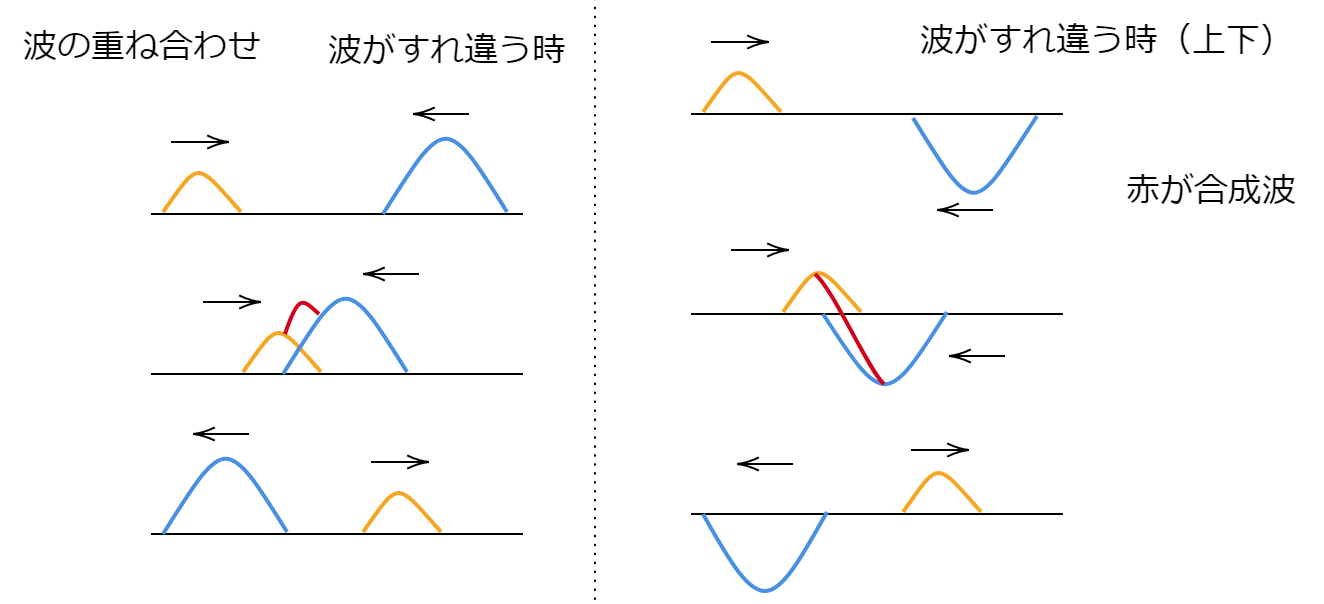
このように波が重なり合う現象をその名の通り、波の重ね合わせといいます。
また、重なった波はその後お互いの影響を受けずにそのまま進みます。これを波の独立性といいます。
波の反射
定常波
定常波において常に振動しない部分を節、振幅が最大になる場所を腹といいます。
定常波の作り方は位相、周期、波長の等しい2つの進行波がお互いに逆向きに進むと出来上がります。
自由端反射と固定端反射
自由端反射とは入射波が壁に当たったとき位相の反転がなくそのまま反射することです。
一方固定端反射は位相の反転があり、入射波を打ち消すように反射が出てきます。
自由端の描き方は波が壁に当たってもそのまま進行すると仮定して波形を描き、それを壁で折り返すと描くことができます。
固定端は位相が逆になるため、自由端反射と同じく波が壁に当たってもそのまま進行すると仮定した後、その波をx軸に対して上下さかさまにして折り返すと書くことができます。
波の干渉
波の干渉とは複数の波が重なり合って、互いに強め合ったり弱めあったりする場所ができる現象のことをいいます。
2つの波の波源からの距離を \(l_1, l_2\) とし、それらの位相がそろっているときに、距離の差 \(|l_1-l_2|\) が波長の整数倍になっていれば、波は強め合います。
$$|l_1-l_2|=m\lambda $$
ただし \(m=0,1,2,…\) です。
一方、波の山と谷が重なったとき弱めあいます。そのとき距離の差が波長の半整数倍になります。
$$|l_1-l_2|=(m+\frac{1}{2})\lambda $$
この2つは後でものすごくよく出てくるので覚えておいて下さい。
ホイヘンスの原理
波面上の各点からそれを波源とする球面波が発生します。
球面波で覚えてほしい現象が1つあり、それがこちらです。
「球面波は波の進む速さと等しい速さで広がり、これら無数の球面波に共通する面が次の瞬間の波面になる。」
というものがホイヘンスの原理です。
知識として覚えていきましょう!
平面波の屈折と干渉
一般に入射角 \(\theta \) と反射角 \(\theta’ \) は等しい。
$$\theta =\theta’$$
これを反射の法則といいます。
入射とは空気中から水に波が進むこと、またガラスの中から空気中に波が戻ってくることなどを言います。
そして次はこちら
入射角と反射角、それに媒質1,2 での波の速さや波長の関係を次式で表せます。
$$\frac{\sin\theta_1}{\sin\theta_2}=\frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2}=n_{12}$$
これを屈折の法則といいます。
\(n_{12}\) は媒質1と媒質2によって決まる一定の値であり、媒質1に対する媒質2の屈折率といいます。
すごくわかりにくいのですが屈折率は
$$\frac{\sin\theta_1}{\sin\theta_2}=\frac{v_1}{v_2}=\frac{\lambda_1}{\lambda_2}=\frac{n_2}{n_1}$$
になります。
屈折率だけ数字が逆になるので注意です!
まとめ
今回は干渉や平面波の屈折について学びました。
忘れやすいのですがしっかり覚えましょう!
次はこちら!3-3音の伝わり方・物体の振動