前回はこちら!2-4熱効率・カルノーサイクル
ここから波について学んでいきます。
身の回りにある波といえば音波や光波などがあると思います。
熱に続いて目に見えない現象を取り扱いますので、しっかりと勉強しましょう!
用語集
| 用語 | 説明 | 用語 | 説明 | |
| 波 | 振動が次々と周りに伝わる現象 | 媒質 | 波を伝える物質 | |
| 波源 | 振動の源 | 波形 | ある瞬間における波の形 | |
| 正弦波 | 単振動によって生じる波形が正弦曲線\(\sin x の形\)になる波のこと | 振幅 | 波の高さのこと | |
| 山・谷 | 波形の最も高いところを山・低いところを谷といいます | 波長 | 山と山の間隔 | |
| 位相 | 振動状態を表す量のことです | 同位相・逆位相 | 位相が同じことを同位相、位相がちょうど逆になっているのを逆位相といいます | |
| 縦波・横波 | 波の進行方向に動く波を縦波、垂直に動く波を横波といいます |
波分野の最初ですので覚えるべき用語が多くなっています!
波の性質と正弦波
ある場所に生じた振動が周りに伝わる現象を波といいます。まずは波形について勉強しましょう。
波形とはある瞬間における波の形のことです。
正弦波
単振動によって生じる波形は正弦曲線になります。
これから正弦曲線をあつかうので、このことは忘れないでください。
ちなみに正弦とは数学で学んだ \(\sin\) 関数のことです。
波の要素
まずは山と谷について説明します。
以下の図を見てください。
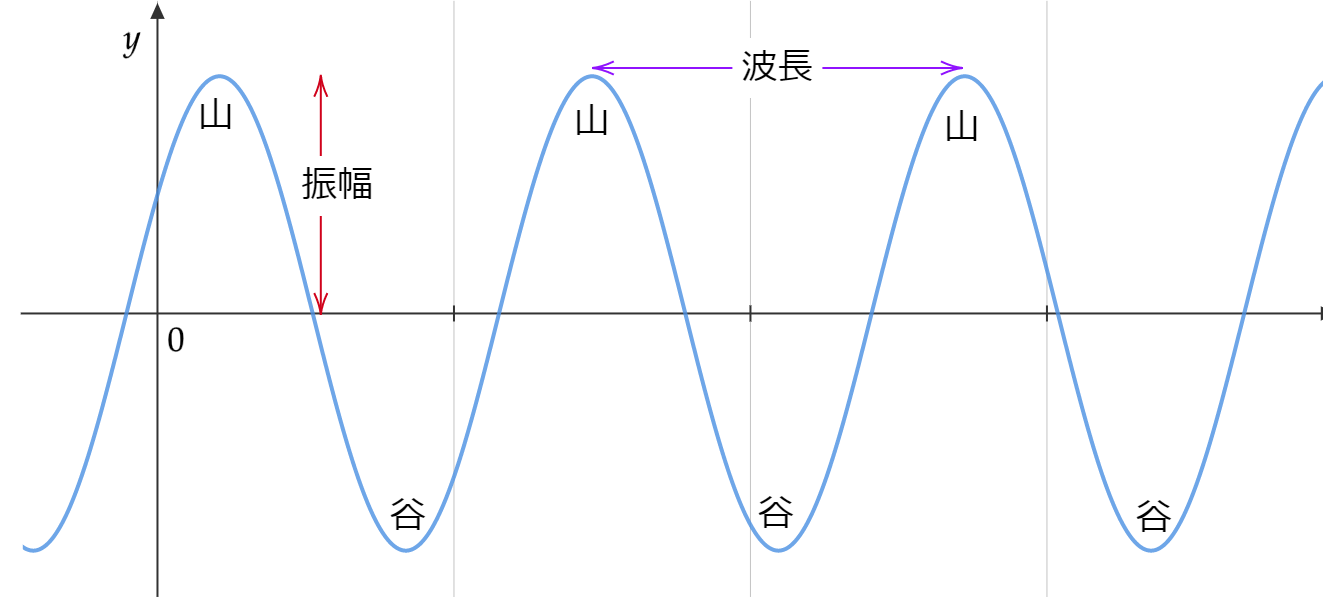
波の振動が一番高くなっている場所を山、一番低くなっている場所を谷といいます。見た目通りですね。
なお、山(谷)の高さを振幅といいます。
山と山の間隔を波長といいます。波長は今後も出てくる重要用語ですので、この定義をしっかりと覚えてください。
波動の分野だけでなく、一番最後に学ぶ原子の分野でもよく出てきます。
位相
位相とは振動状態を表す量です。
同じ振動状態を同位相、逆の振動状態を逆位相といいます。下の図のような振幅と時間の関係図を確認しましょう!
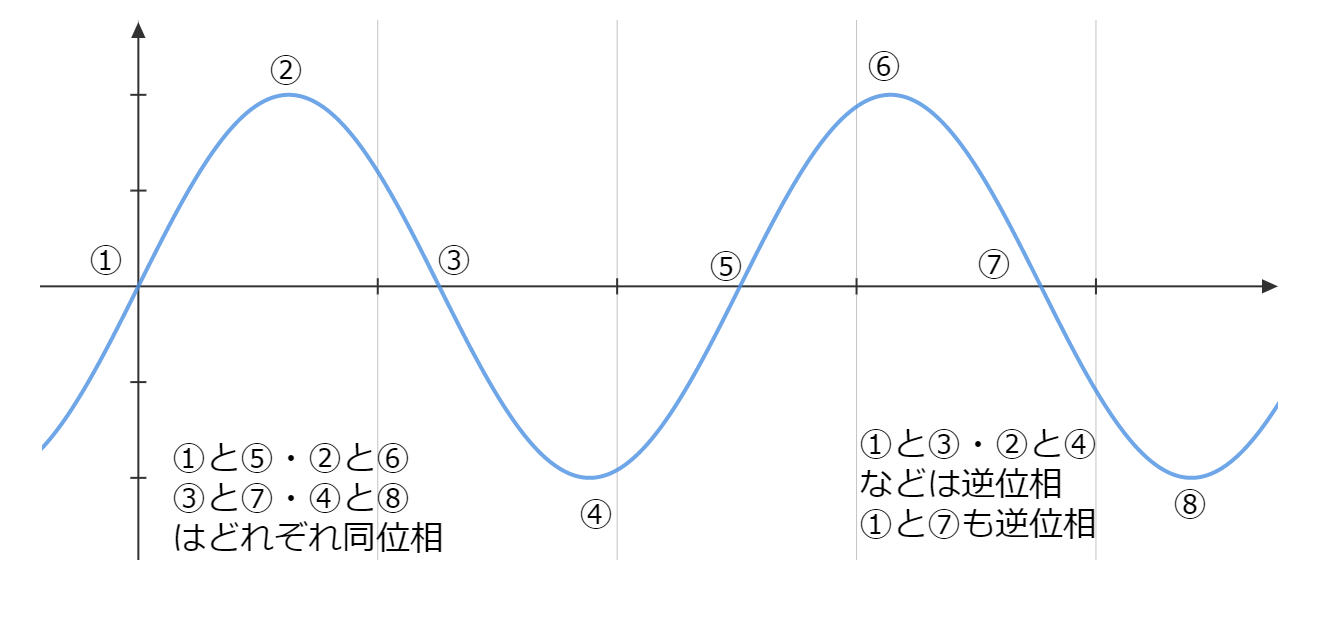
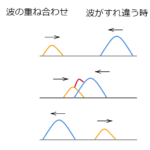
同位相の波が重なると1つになって強い波(振幅が大きい)ができます。
一方逆位相の波が重なると、弱い波(振幅が小さい)ができます。
特に、波長や振幅が全く同じ波を逆位相の関係で重ねると、打ち消しあいます。
縦波と横波
先に横波を学びましょう。
横波(よこなみ)は波の進行方向に対して垂直な方向に振動する波のことを言います。例として電磁波が挙げられます。
波の進行方向に振動する波を縦波(たてなみ)といいます。例として音波が挙げれれます。
知識として覚えておいてください。
正弦波の式
正弦波の式は
$$y=A\sin\frac{2\pi}{T}(t-\frac{x}{v})=A\sin 2\pi(\frac{t}{T}-\frac{x}{\lambda})$$
で表されます。
簡単に説明します。原点 O の媒質が
$$y=A\sin\omega t$$
で表される単振動をしているとします。
原点での振動が位置 \(x\) に達するまでに要する時間は \(\frac{x}{v}\) で表せます。つまり位置 \(x\) の媒質は \(\frac{x}{v}\) 遅れて原点と同じ振動します。
時刻 \(t\) における位置 \(x\) の媒質の変位を \(y\) とすると \(y\) は時刻 \(t-\frac{x}{v}\) で、原点での変位に等しくなります。
したがって
$$y=A\sin\omega (t-\frac{x}{v})$$
となります。また、各振動数 \(\omega\) を \(\omega =\frac{2\pi}{T}\) とおくと次のようになります
$$y=A\sin 2\pi (\frac{t}{T}-\frac{x}{\lambda})$$
最後は \(vT=\lambda\) の関係です。これは「速さ \(\mathrm{m/s}\) ×時間 \(\mathrm{s}\) = 波長 \(\mathrm{m}\)」です。
まとめ
今回は波の性質について学びました。
新たな用語をしっかり覚えましょう!
次はこちら!3-2重ね合わせの原理・波の反射・干渉