数学の話をします。
物理において数学は道具として必須です。
しかし、高校物理で数学のどの知識が必要なのかわからずに取り組むよりも、あらかじめ知ってから取り組んだ方が効率が良いと思います。
数学の知識は必要?
物理を学ぶうえで数学の知識は必須です。
高校物理において必須なのは
「2次関数」「ベクトル」「三角関数」
などです(ほかにもありますが書ききれないのでここでは3つだけ)。少し難しい入試問題では
「数列」「指数・対数」
などの知識が必要になります(あくまで基礎レベルで十分)。そして大学で学ぶ物理では
「微分積分」「線形代数(行列など)」「複素数」
などが必要です。
しかし、これらは一例で、他の数学の分野とも密接なかかわりがあります。
このページでは大学入試において最低限覚えてほしい数学の知識を説明していきたいと思います!
最低限知ってほしい基礎知識
ギリシア文字の読み方
物理にもたくさん出てきますが、数学にもギリシア文字出てくるので、よく出てくるギリシア文字の読み方をここで説明します。
| 文字 | 説明 | 文字 | 説明 |
| \(\alpha\) | アルファ(エーではない) | \(\beta\) | ベータ(ビーではない) |
| \(\gamma\) | ガンマ (原子分野の放射線の話で出てくる) |
\(\Delta\) | (大文字の)デルタ (微小変化など) |
| \(\epsilon\) | イプシロン(電磁気分野で出てくる誘電率など) | \(\theta\) | シータ(三角関数で出てくる) |
| \(mu\) | 摩擦係数などではミューと読む。 接頭語で使うときはマイクロと読み、その値は\(10^{-6}\) |
\(\lambda\) | ラムダ(波長など) |
| \(sigma\) | シグマ(電気伝導率など) | \(\omega\) | オメガ(力学の角振動数など) |
このほかにも重要な文字はたくさんあります。
それらは出てきたら読み方を調べてその都度覚えればよいと思います!
二次関数
二次関数は様々な分野で出てきます。力学の分野で出てくる運動エネルギーは速さの二乗に比例しているので二次関数ですし、弾性エネルギーも基準点からの変位の二乗に比例しています。
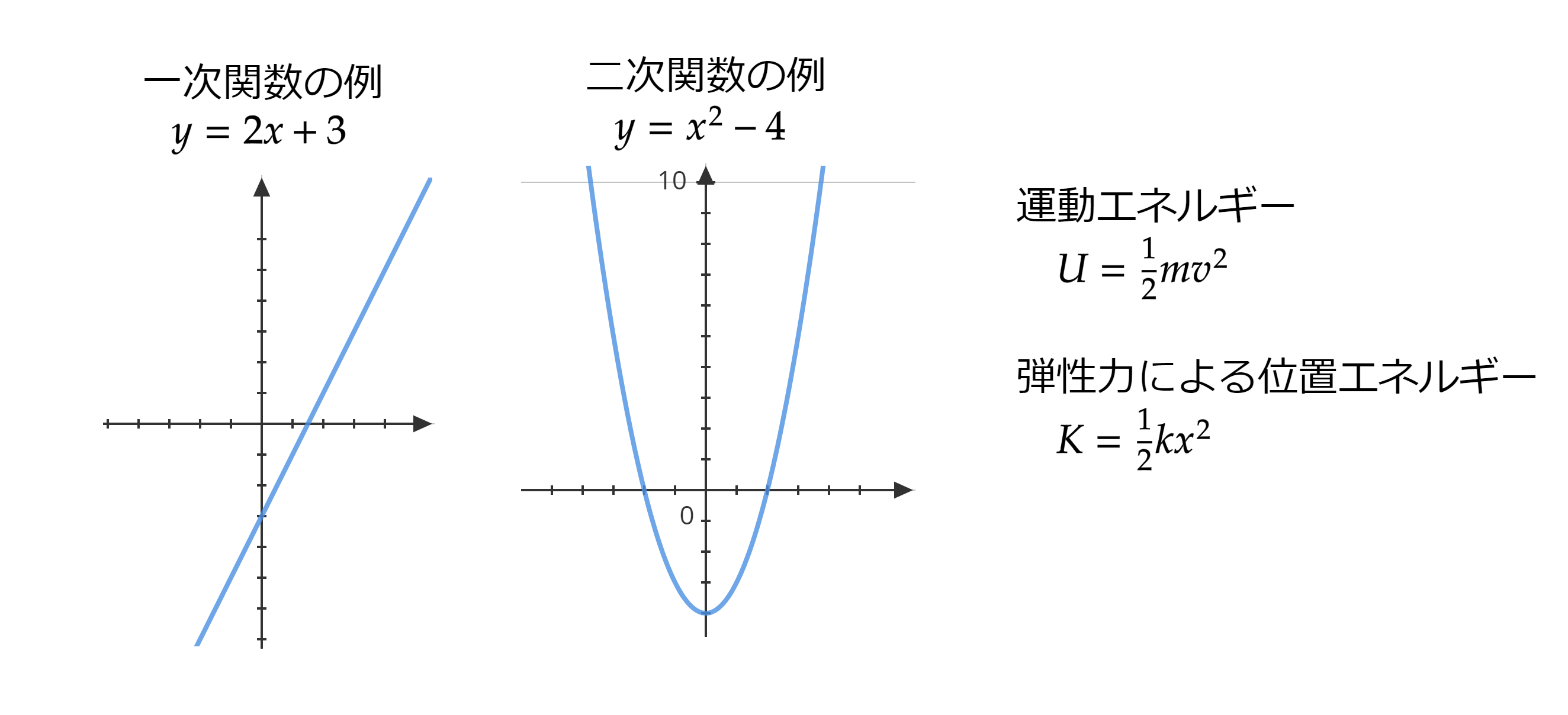
ここでは二次関数の中でも、平方完成のみを取り扱いたいと思います。
平方完成を覚えていますか?こんな感じでしたね。
$$ax^2+bx = a\(x+\frac{b}{2a}\)^2-a\times\(\frac{b}{2a}\)^2$$
平方完成は2次関数の頂点の座標を求めるときや変数 \(x\) を一か所に集めたいときに使います。
ここは物理学をメインに説明するサイトなのでうまくできるかわかりませんが、平方完成のやり方を一応説明してみます。
まず(なんでもいいですが)変数xの2次式と1次式があったとします。
$$x^2+6x$$
突然ですがここで\(\(x+3\)^2\)という式を考えます。これを展開すると
$$\(x+3\)^2=x^2+6x+9$$
$$x^2+6x=\(x+3\)^2-9$$
$$x^2+6x=\(x+\frac{6}{2}\)^2- \(\frac{6}{2}\)^2 $$
これを一般化するとこうなります
$$x^2+ax=\(x+\frac{a}{2}\)^2-\(\frac{a}{2}\)^2$$
はい。こんな感じです。
力学の最初に学ぶ位置xの式\(x=v_0t+\frac{1}{2}at^2\)を例に平方完成をしてみましょう。
$$x=v_0t+\frac{1}{2}at^2$$
まず見やすくするために右辺と左辺を入れ替えます。(個人的に入れ替えた方が見やすいと思っただけなので別にこの操作は必要ではないです。)
$$\frac{1}{2}at^2+v_0t=x$$
では平方完成をしましょう。
$$\frac{1}{2}a\(t+\frac{v_0}{a}\)^2-\frac{1}{2}a\times\(\frac{v_0}{a}\)^2=x$$
最後に適当に整理して、
$$\frac{1}{2}a\(t+\frac{v_0}{a}\)^2-\frac{v_0^2}{2a}=x$$
はいできました。
高校物理における平方完成はグラフを書くため…というより式を導出するときに使います。
これができなければ絶対に問題が解けない!…ということはめったにないと思いますが、平方完成は数学1の基本ですので是非マスターしましょう!
三角関数
物理を学ぶうえで三角関数の知識は非常に重要です。
数学の授業でsinとか\cosを勉強したとき何の役に立つのかわかりませんでしたが、これらは物理の役に立ちます。それもものすごく役に立ちます。
まず三角関数の定義を復習しておきましょう
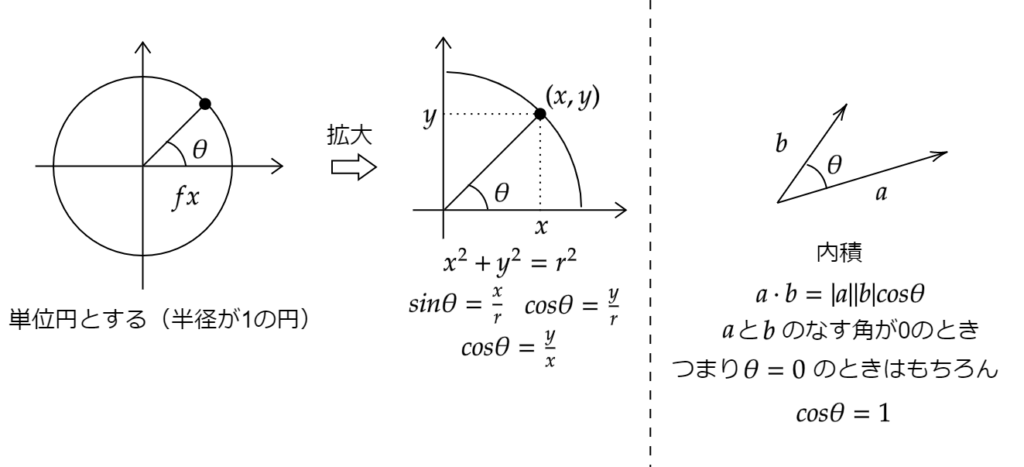
単位円を考えます(半径が1の丸い円)
その円上に点\(x,y\)があるとき \(sin\theta\) を \(\frac{x}{r}\) 、 \(\cos\theta\) を \(\frac{y}{r}\) と定義します。(ただし \(r^2=x^2+y^2\) )
これは定義です。忘れてはいけません。
ベクトル
ベクトルの合成
ベクトルの合成と内積について取り扱います。
ベクトルの合成は座標を見ればわかりやすいと思います。
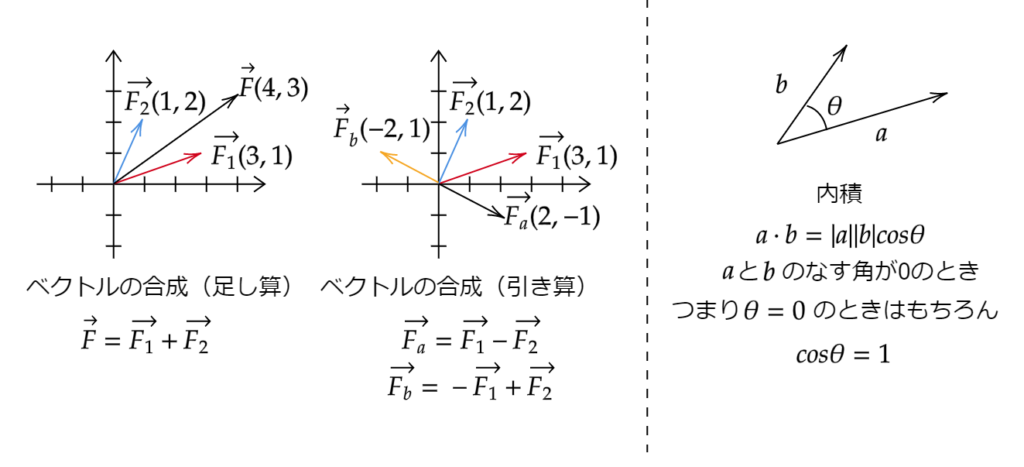
\(\vec{F_1}\)\(3,1\)と \(\vec{F_2}\)\(1,2\)の合成は
$$\(3,1\)+\(1,2\)=\(4,3\)$$
になります 。座標に注目すれば簡単ですね。
実はベクトルの引き算も座標に注目すれば簡単にできます。
ベクトルの内積
ベクトルの内積はいわば、ベクトルの掛け算のようなものであり、「・」を使って表します。
ベクトルの内積は以下のように定義され、結果はスカラー(向きを持たない大きさだけの量)になります。
$$\vec{a}\cdot\vec{b}=| \vec{a}|| \vec{b} |\cos\theta$$
$$\vec{a}\(a_1,a_2\)\cdot\vec{b}\(b_1,b_2\)=\(a_1+b_1,a_2+b_2\)$$
2通りの計算方法がありまして、これらは状況に合わせて使い分けます。
ちなみに物理でよく出てくるのは()の方です。
aベクトルとbベクトルの向きが同じのとき、\cosθの値はいくつになるでしょうか?
三角関数の基礎が分かっていれば答えられると思います。(答えは1になります)
近似式
あまり出てきませんが近似式の話をします。
近似とは細かい値を無視しておおよその値で表そうという考えで、簡単な例を挙げると
$$3.000001 \times 1.999999$$
という掛け算をするのはめんどくさいのでこれを \(3\times 2\) とみなして計算することです。
近似式で有名な式はこちらです。
\(|x|ll1\)のとき\(\(1+x\)^n \\approx 1+nx\)
「例9」xに0.01、nに2を代入してみましょう。まず右辺は
$$1+2\cdot0.01=1.02$$
一方左辺を展開すると
$$\(1+0.01\)^2 =1+2\cdot1\cdot0.01+0.01^2 =1.02+0.01^2 =1.02+0.0001 $$
ここで1.02と0.0001を比べてみると…
1.02に比べて0.0001なんて小さいので無視してもよくないですかね?
よし、無視しましょう!そうすると左辺も1.02になりますね。これが近似です。
内分と外分
内分と外分です。重心の話で出てきますので思い出しましょう!
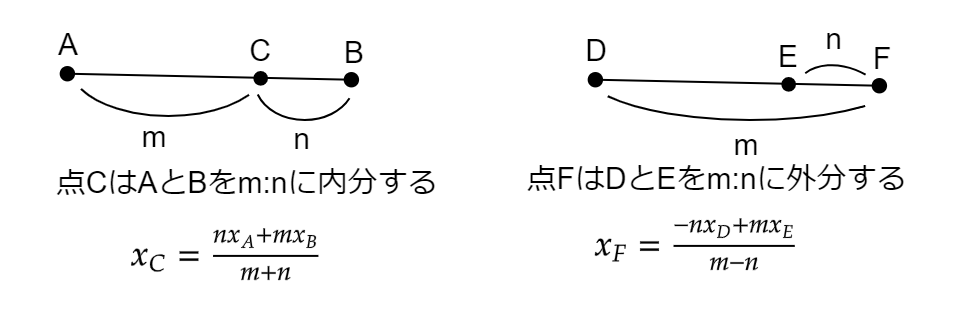
内分と外分の定義は上の図のようになっています。
まとめ
何回も言いますが、物理を学ぶうえで数学は重要です。
そしてこのページはあくまで最低限の知識しかのせていません。
是非ともマスターしてください!




