前回はこちら!1-3.剛体に働く力・モーメント
ここでは力のつり合いの例として、弾性力、浮力、垂直抗力などを取り扱います。
しっかりと図を書いて、力の向きを考えましょう!
用語集
必要な用語を書いていきます。
| 名前 | 説明 |
| ばね定数 | 「k」で表すことが多く、ばねの伸び縮みやすさを表します。値が大きければ伸び縮みしにくいということを意味します |
| 圧力 | 「p」で表すことが多く、単位面積あたりに働く力を意味します |
| 浮力 | 浮く力。物体の上側と下側に加わる圧力の差から生じます |
| 垂直抗力 | 接触している固体を押し返す力です |
| 粗い面 | 摩擦があるということを意味します(一応覚えてください…) |
しっかりと覚えましょう!
力のつり合い
力のつりあいとは物体に働く力のベクトルが打ち消しあい、物体が平行運動も回転運動もせずに、静止する状態のことを言います。
力のつり合いは図に矢印を書き込んで、力がどこに働いているのかを分かりやすくすることが肝心です。
図を描くことができれば水平方向、鉛直方向に対して式を立てればokです。
弾性力
ばねが伸び縮みしたときに働くことを意味した、フックの法則がこちらです。
$$F=kx$$
\(k\) はばね定数と呼ばれます。ドイツ語で定数を意味する [Konstante]の頭文字であるといわれています(諸説あり)。
\(F\) は力です。これはそのままなので良いのですが、 \(x\) に気を付けてください。
\(x\) はつり合いの位置からの変位です。ばね全体の長さではないので注意!!!
下の図で確認しましょう!
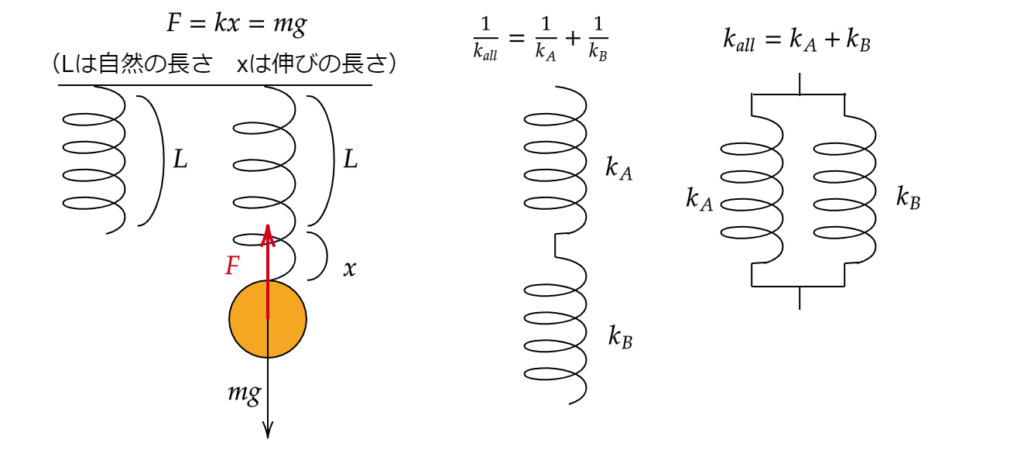
ばねを複数つなげることを、よくばねの合成と言います。
ばねの合成については上図の右側に2つだけ載せました。
直列型のばね定数 \(k_{all}\) の計算はできますでしょうか。意外と戸惑いやすいので計算だけやってみましょう。公式はこんな感じです。
$$\frac{1}{k_{all}}= \frac{1}{k_A}+\frac{1}{k_B}$$
通分します。
$$\frac{1}{k_{all}}= \frac{k_B}{k_A\cdot k_B}+\frac{k_A}{k_A\cdot k_B}$$
$$\frac{1}{k_{all}}=\frac{k_A+k_B}{k_A\cdot k_B}$$
最後に逆数を取って
$$k_{all}=\frac{k_A\cdot k_B} {k_A+k_B} $$
はい。できました。
並列型は何個並んでも足せばいいだけです。式で書くと次のようになります。
$$k_{all}=k_1+k_2+k_3+\cdots+k_n$$
簡単ですね。
圧力
圧力は[pressure]の頭文字をとって \(p\) で表すことが多いです。
$$pS=F$$
この式は(圧力[Pa]×面積[m^2]=力[N])を意味しており、圧力の単位は[Pa]パスカルで表します。
数式から判断できるのですが、圧力は単位面積あたりに加わる力の大きさを表しています。
「大気圧」の話もついでにしましょう。地球上の大気(空気)が物体や我々人間に加える圧力のことで、地上では約\(1.0×10^5\)Paです。
天気予報などではもう少し詳しい値の1013hPaで表すことが多いです。
(hは「ヘクト」と読み、100倍の意味です。)
この圧力は次の浮力の話で活躍します。
浮力
浮力とはその名の通り浮く力です。
浮力の式は間違えやすいので注意!! 式はこちらです
$$F=mg=\rho Vg$$
ここで出てくる \(\rho\) は「ロー」と読み、水の密度を表しています。物体の密度を表しているわけではないので注意!
しかし、\(V\) は水ではなく、物体の体積を表しています!
間違えやすいので注意。

浮力は物体の上側の圧力 \(F_1\) と下側にかかる圧力 \(F_2\) の差から生じます。
上の右側に図を載せました。
式は見ての通りですが2点ほど気を付けましょう。
- 密度は慣習的に \(\rho\) (ロー)で表します。圧力を表す \(p\) (ピー)と見間違えないように注意
- 先ほどの圧力の話で出てきた \(F=pS\) を忘れてはならない
浮力は理解しにくいとは思いますが、圧力の差であるということに注目して理解しましょう!
作用反作用
2つの物体の間で及ぼしあう一方の力を「作用」もう一方の力を「反作用」といいます。
反作用は作用と力の大きさが同じで、向きが同一作用線上に真逆に働きます。
また、重力や静電気力などの遠隔力に対しても成り立ちます。
垂直抗力と摩擦力
垂直抗力は作用反作用によって引き起こされます。
物体が地面を押す力(重力)を作用とした時、その反作用が垂直抗力となります。
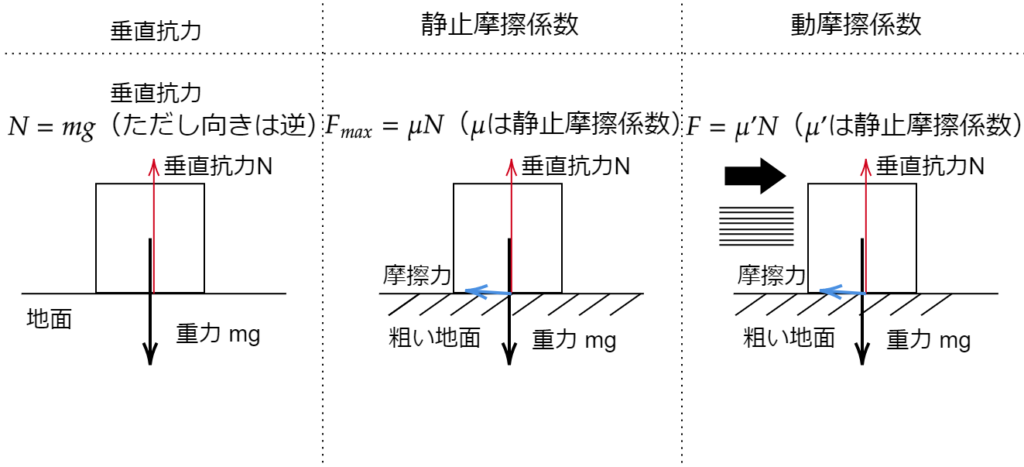
問題文に「粗い面」と書かれていたら摩擦があると考えましょう。(これはお約束みたいなものです。)
静止・動摩擦係数は「係数」と書かれている通り、一定の値です。物質によって決まっています。
なお、式にあるとおり、摩擦力は垂直抗力 \(N\) に依存します。
静止・動摩擦力係数は問題文に書いてあることが多いのでいちいち値を覚えなければいけないということはありません。
もし書いていなくても、問題文から計算して求められます。
問題
ばねに関する問題を解いてみましょう。

解答いきます。
並列の場合そのまま足し算をすればよいでしたね。
並列部分では
$$k_{AB}=k_A+k_B$$
直列部分を考えると
$$\frac{1}{k_{all}}=\frac{1}{k_{AB}}+\frac{1}{k_C}$$
$$\frac{1}{k_{all}}=\frac{k_{AB}+k_C}{k_{AB}k_C}$$
$$k_{all}=\frac{k_{AB}k_C}{k_{AB}+k_C}$$
$$k_{all}=\frac{(k_A+k_B)k_C}{k_A+k_B+k_C}$$
となります。
まとめ
今回は力のつり合い、摩擦などについて学びました。
ここでは最初に書いた通り図を書いて、力の向きを考えることが重要です。
問題演習を通してしっかり身につけましょう!
次はこちら!1-5運動方程式