前回はこちら!1-9単振動
ここではケプラーの法則・万有引力の法則について学びます。
ケプラーの法則は直接問われることは少ないのですが、証明問題の途中に使ったりします。
また、一度は聞いたことがある万有引力の法則を数式で表して、これを利用して第1・第2宇宙速度を計算ししょう。
用語集
直接問われることはないと思いますが、しっかり覚えましょう!
| 用語 | 説明 |
| 天動説 | 地球を中心として周りの天体が動いていると考えること |
| ケプラーの第一法則 | 惑星は太陽を一つの焦点とする楕円軌道を描く |
| ケプラーの第二法則 | 面積速度一定の法則。惑星と太陽を結ぶ線分が、一定時間に描く面積は一定である |
| ケプラーの第三法則 | 惑星の公転周期の2乗は楕円軌道の半長軸の3乗に比例する |
| 万有引力の法則 | 二つに物体間に働く力はそれぞれの質量の積に比例し、距離の二乗に反比例する |
| 第一宇宙速度 | 地表近くを円軌道を描いて回る物体の速度 |
| 第二宇宙速度 | 地球から飛び去るために必要な最小限の速度 |
では内容に入ります。
ケプラーの法則
ケプラーの第一法則
第一法則:惑星は太陽を一つの焦点とする楕円運動を描くというものです。
(入試に直接出ることはあまりないですね・・・。)
ここでは重要ではありませんが楕円の式は \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) で表されます。
ケプラーの第二法則
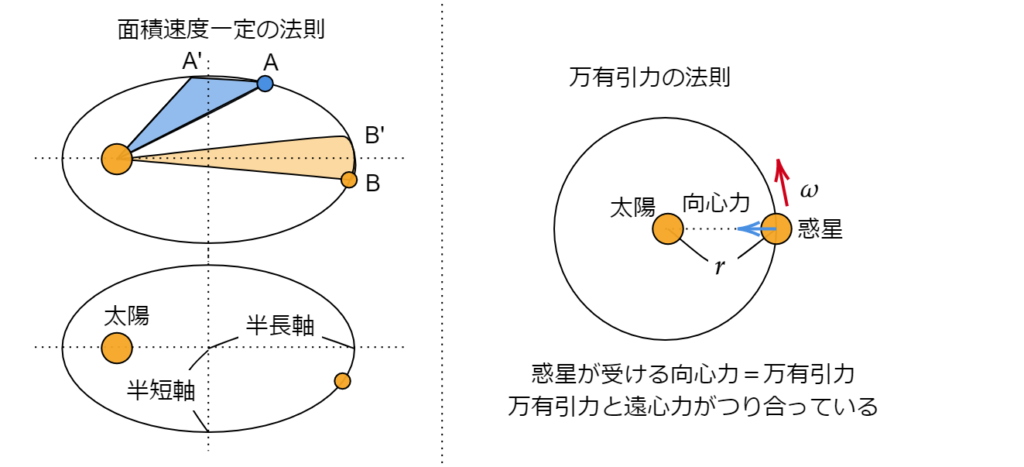
第二法則は面積速度一定の法則です。
これは一定時間に描く「太陽」「惑星の初期位置」「\(t\) 秒後の惑星の位置」の三点を頂点とした三角形の面積がどこでも一定であるというものです。
下の図で、青い惑星 A が A’ に移動する時間をtとします。そして同じ軌道に乗っているオレンジの惑星 B が \(t\) 秒間かけて B’ にたどり着いたとき、青い面積とオレンジの面積は等しくなるというものがこの第二法則です。
万有引力
万有引力は二つに物体間に働く力はそれぞれの質量の積に比例し、距離の二乗に反比例する。
というものです式はそのままで
$$F=G\frac{m_1m_2}{r^2}\tag{1}$$
式に出てきた \(G\) は万有引力定数と呼ばれその値は
$$G=6.67\times 10^{-11}\tag{2}$$
です。この値は覚える必要はないでしょう。
万有引力の式を導出してみましょうか。
また運動方程式を変形します
$$F=ma=mr\omega^2=mr(\frac{2\pi}{T})^2\tag{3}$$
(ただし \(m\) は惑星の質量)
円運動で覚えてほしい\(a=r\omega^2\)の関係は覚えていますでしょうか?忘れていたら復習しましょう!
さらにそれを公転周期の二乗が半長軸の三乗に比例する「ケプラーの第三法則 \(T^2=kr^3\) 」を用いると
$$F=\frac{4\pi^2m}{kr^2}\tag{4}$$
こうなります。(ただし k は定数)
ここで作用反作用の法則より太陽も同じ力を受けます。
$$F=\frac{4\pi^2M}{kr^2}\tag{5}$$
(ただし \(M\) は太陽の質量)これらを同時に満たすには
$$F=G\frac{Mm}{r^2}\tag{6}$$
としなければいけません。よって万有引力が導かれました。
さて、もちろん万有引力は地球上でも働いているので今まで使ってきた重力加速度 \(g\) と
$$mg=G\frac{Mm}{R^2}\tag{7}$$
が成り立ちます。この式から地球上の物体の質量 \(m\) を消すと
$$gR^2=GM\tag{8}$$
が導かれます。この式は次の宇宙速度の話で出てきます。
第一宇宙速度・第二宇宙速度
第一宇宙速度
第一宇宙速度とは地表近くを円軌道を描いて回る物体の速度のことです。
これは運動方程式を立てればわかります。
$$m\frac{v^2}{R}=G\frac{Mm}{R^2}\tag{9}$$
左辺は等速円運動するときの加速度と速度の関係式\(ma=m\frac{v^2}{r}\)をそのまま使いました。右辺は万有引力の式で、両辺に出てくる \(R\) は地球の半径です。この方程式と式\(8\)より
$$\frac{v^2}{R}=\frac{gR^2}{R^2}\tag{10}$$
$$v=\sqrt{gR}\tag{11}$$
になります。これが第一宇宙速度です。
万有引力による位置エネルギー
力を微分すればエネルギーになるので
$$U=\frac{d}{dr}F=\frac{d}{dr}(G\frac{Mm}{r^2})=-G\frac{Mm}{r}\tag{12}$$
となります。
第二宇宙速度
第二宇宙速度とは地球から飛び去るために必要な最小限の速度のことです。
これは地球から宇宙に向けて発射する「ロケットが持つ運動エネルギー」が「万有引力によるエネルギー」を超えればロケットが地球から飛び去れます。
ということで
$$\frac{1}{2}mv^2_0>G\frac{Mm}{R}\tag{13}$$
$$v_0>\sqrt{2gR}\tag{14}$$
になります。先ほどと同様\(8\)式を利用しました。
問題
では一問問題を解いてみましょう。
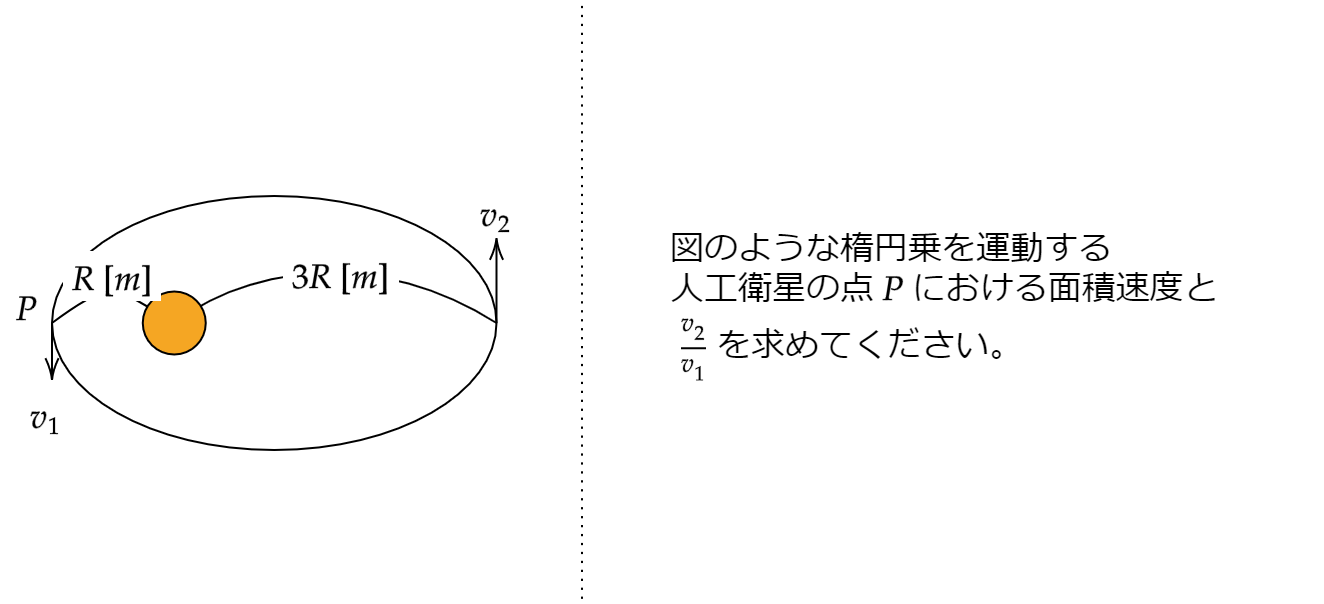
では答えを書いていきます。
万有引力による運動では面積速度が一定です。
そのため
$$\frac{1}{2}Rv_1$$
単位は [m^2/s] です。
もう一つの速度の比を求めてみましょう。
面積速度は一定ですので
$$\frac{1}{2}Rv_1=\frac{1}{2}2Rv_2$$
$$\frac{v_2}{v_1}=\frac{1}{2}$$
です。
まとめ
今回はケプラーの法則や宇宙速度について学びました。
それぞれの言葉の意味を直接入試で問われることはあまりないのですが、言葉を理解していれば問題がグッと解きやすくなるはずです。
しっかりと覚えてから問題に取り組みましょう!
次回は熱理学!高校熱力学全体概要