ここから磁場の話をします。
電流とものすごーく関係があります。
電気はできるけれど磁気は苦手…という方が多いのでしっかりと学びましょう!
磁場
磁石の両端には磁極があります。
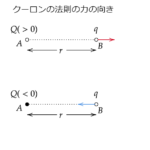
磁極はN極とS極の2つがあり、同じ極どうしでは斥力(反発する力のこと)が働き、
異なる極の場合、引力が働きます。
磁極の強さを表す量は磁気量と呼ばれ、N極の場合プラス、S極の場合マイナスになります。
さて、ここで電気分野で出てきたクーロンの法則と同じ形をしている式が登場します。
$$F=k_m\frac{m_1m_2}{r^2}$$
これを磁気力に関するクーロンの法則と呼びます。(mは磁化の大きさ)
磁場
磁極が磁気力を受ける空間には磁場が広がっているといいます。
磁場の中のある位置1WbのN極を置いた時、この磁極が受ける力の向きを磁場の向き、大きさを磁場の強さとします。
磁場の強さの単位はやや聞きなれない言葉になります。
それがこちら「[N / Wb] ニュートン毎ウェーバ」です。
磁場は電場と同じくベクトルです。
電場中に電荷を置くと力を受けましたよね。
$$\vec{F}=q\vec{E}$$
磁場も同じです。磁場 \(H\) に磁気量 \(m\) [Wb]の磁化を置いた時、磁気力 \(F\) は
$$\vec{F}=m\vec{H}$$
となります。
電流と磁場
さて、電流と磁場を紐づける超重要な話をします。
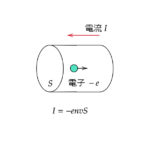
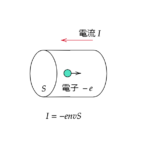
それは電流が流れるとその周りには磁場が発生するというものです。
これには向きがあり、電流が流れる方向と発生する磁場の方向は右ねじと同じ関係にあります。
右ねじ・・・といわれてピンときますかね?
ネジというものは基本的に右回し、つまり時計回りにドライバー(ねじを締める道具)を回せば締まります。
そこから右ねじの法則と名付いています。
その磁場の強さは次式で表されます。
$$H=\frac{I}{2\pi r}$$
磁場の強さの単位は A/m で表されます。日本語で書くと「アンペア毎メートル」です。
上の式を見ればわかるかと思います。分母の \(2\pi\) は定数ですよね。
分子は電流ですので単位は [A] アンペア、分母は距離ですので [m] が単位です。
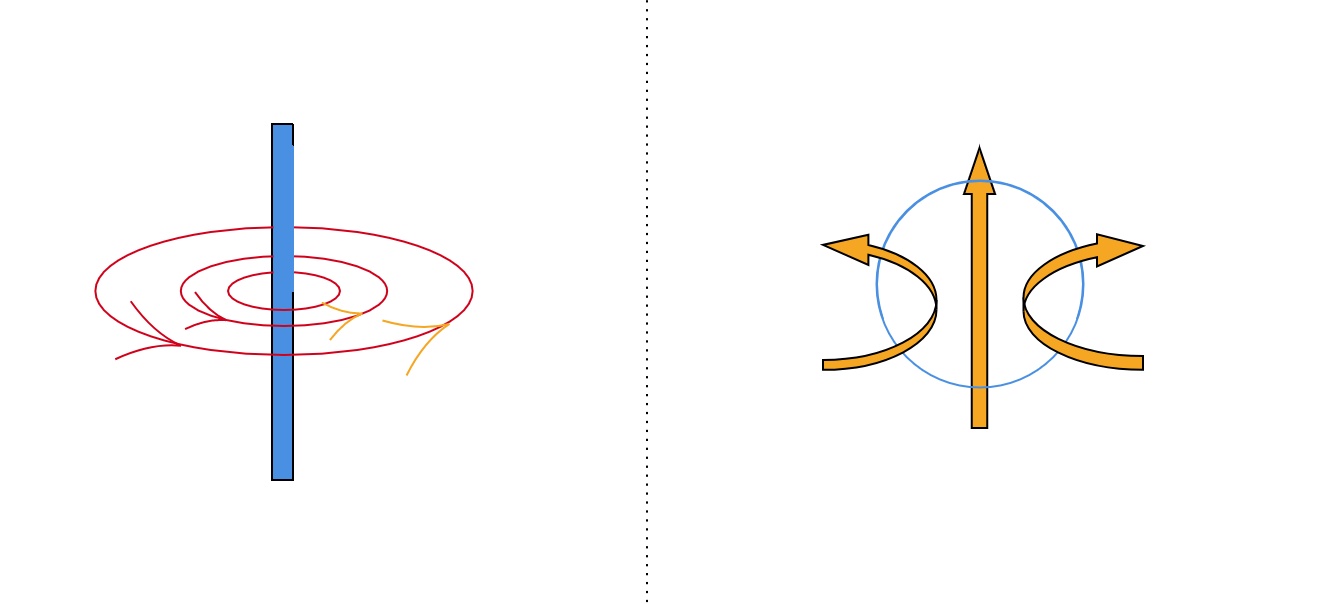
今度は直線ではなく、円形の電流が作り出す磁場を考えていきましょう。(上の右図)
半径 \(r\) の円形の導線に電流を流すとき、その中心の磁場の強さは
$$H=\frac{I}{2r}$$
導線の巻き数が N のとき円の中心の磁場の強さは
$$H=N\frac{I}{2r}$$
となります。
次にソレノイドを考えます。
ソレノイドとは導線をらせん状に巻き、十分に長い円筒状にしたコイルのことを指します。
ソレノイドの内部の磁場の強さは一定になります。
$$H=nI$$
シンプルですね。\(n\)はコイルの巻き数です。
まとめ
今回は磁場が出てきました。
電磁気分野の後半のメインキャラクターが磁場になります。
導線に電流が流れると磁場が発生することは忘れないでください!