前回はこちら!
フレミングの左手の法則とローレンツ力を中心に見ていきます。
磁場の強さを表す \(H\) と磁束密度 \(B\) の違いをしっかり見ましょう!
用語集
ややこしい用語が増えますがしっかり覚えましょう!
| 用語 | 説明 | 用語 | 説明 |
| フレミングの左手の法則 | 電流と磁場とそれに働く力を左手で表した法則 | 磁化 | 磁場を印加すると磁石の性質を持つ物体 |
| 透磁率 | 物質によって決まる定数で、磁束の通りやすさを表す | 強磁性体 | 磁場を印加するとその方向に強く磁化する物体 |
| 常磁性体 | 磁場を印加すると磁場の向きに少しだけ磁化する物質 | 反磁性体 | 磁場を印加すると磁場とは逆向きに磁化する物体 |
| 磁束密度 \(B\) | 物質の透磁率も含めた磁場の様子を表します | ローレンツ力 | 電荷をもつ粒子が磁場の中を動くときに受ける力 |
フレミングの左手の法則
左手の親指、人差し指、中指をそれぞれ垂直な関係になるようにした時
$$F=\mu IHl\tag{1}$$
が成り立ちます。
比例定数 \(\mu\) は透磁率と呼ばれます。
\(I\) [A] は電流で単位は アンペア。\(H\) [A/m] は磁場の強さ。\(l\) は今考えている導線の長さです。
透磁率とは磁束の通りやすさを表している物質に固有の定数です。
しかし(1)は電流と磁場が垂直な場合の式です。
これらが垂直でない場合はどうなるのでしょうか?
電流と磁場のなす角を \(\theta\) とすると
$$F=\mu IHl\sin\theta\tag{2}$$
となります。
磁化・磁束
磁化
外部から印加されている磁場によって磁石の性質を帯びることを磁化といいます。
また、磁場を取り除いても磁化されたままの物質を強磁性体といいます。
強磁性体は一般に透磁率が大きいことが知られています。
また、磁場を印加した時、少しだけ磁化される物質を常磁性体といいます。
ややこしいのが反磁性体です。
反磁性体は磁場を印加すると磁場の向きとは逆に磁化される物質のことです。
下図で確認しましょう。
磁束密度
物質の透磁率も含めた磁場の様子を磁束密度といいます。
磁束密度は \(B\) で表され
$$B=\mu H\tag{3}$$
で表されます。
単位を見てみましょう。
磁束密度は [T] テスラで表されます。アメリカの電気技師、発明家であったテスラの名前からとっています。
先ほどの(1)式を \(B\) を使って表すと
$$F=IBL\tag{4}$$
となります。
電流が流れている平行な導線に働く力
2つの平行な導線に電流が流れているとします。
これ等に働く力の大きさは
$$F=\mu_0 \frac{I_1I_2}{2\pi r}l\tag{5}$$
となります。
簡単に導出しましょう
導線を流れている電流1が電流2に作る磁場 \(H_1 , B_1\) をまずは求めます。式(3)より
$$B_1=\mu_0H_1=\mu \frac{I_1}{2\pi r}\tag{6}$$
では電流2が受ける力の大きさを考えましょう。式(4)より
$$F=I_2B_1l=mu_0\frac{I_1I_2}{2\pi r}l\tag{7}$$
です。
ローレンツ力
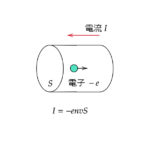
電荷をもつ粒子が磁場の中を動くときに売っ蹴る力をローレンツ力といいます。
電荷1個が受けるローレンツ力は次の式で表されます。
$$f=qvB\tag{8}$$
速度と磁場のなす角が \(\theta\) であるとき、このローレンツ力の式が少し変わってきます。
$$f=qvB\sin\theta\tag{9}$$
このようになります。
なお、電子の場合は \(q\) が \(-e\) になります。
マイナスがつくので気を付けましょう!
まとめ
今期は電場と磁場と力の関係を見ていきました。
問題としてよく出てきますのでぜひマスターしましょう!
次はこちら!