今回は電子の運動やオームの法則について学びます。
オームの法則を導けるようになりましょう!
オームの法則
オームの法則は電気抵抗と電流、電圧の関係を式としてあらわしたものです。
式そのものは意外とシンプルで、
$$RI=V$$
です。
これは中学校でも習っているので見たことがあるはずです。
今回は電子の運動からこのオームの法則を導けるようになりましょう!
抵抗率
オームの法則を導く前に抵抗率について学びましょう。
抵抗率とは物質の材料によって決まっている値で、\(\rho\) (ロー)で表されます。
$$R=\rho \frac{l}{S}$$
単位は [ Ω・m ](オームメートル)です。
断面積 S が大きくなれば電子が通りやすくなるので抵抗 \(R\) が下がります。
抵抗率の温度変化
実はこの抵抗率は温度に依存します。
温度が大きければ大きいほど電子が激しく運動するので動いている電子にぶつかる可能性が高くなります。そのため、電流は流れにくく(抵抗が大きく)なります。
式で表すとこんな感じです。
$$\rho =\rho_0 (1+\alpha t)$$
ここで出てきた \(\alpha\) は物質によって決まっている定数です。
電子の運動
電荷と電流の関係を学びましょう。
電流の正体は電荷の移動です。
式で表すと、
$$I=\frac{q}{t}$$
導線の任意の断面積を時間 \(t\) 秒間に \(q\) の電気量が通過するとき、電流の大きさは上式で表されます。
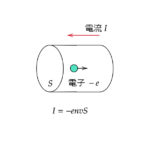
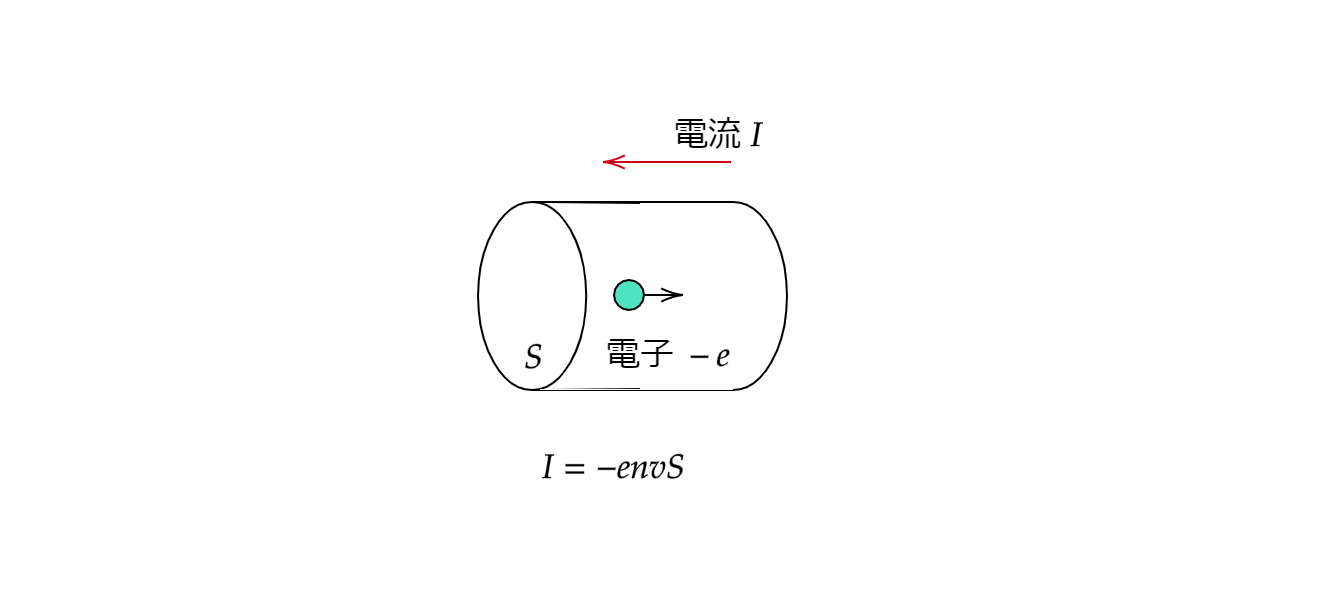
断面積 \(S\) の導線において電気量 \(-e\) の自由電子が1m^2 あたりに \(n\) 個あり、一定の速さ \(v\) で移動しているとき
$$I=envS$$
ここからオームの法則を導きます。
自由電子が断面積 \(S\) 長さ \(l\) の導体の中を一定の速さ \(v\) で移動したとき、抵抗力を受けます。
力が釣り合っているとき、その比例係数を \(k\) とすると
$$eE=kv$$
になります。
また、\(El=V\)(\(l\) は距離)
ですので \(v =\) の式に変換してみると
$$E=\frac{kv}{e}$$
$$E=\frac{V}{l}$$
この2つを合体させて
$$\frac{kv}{e}=\frac{V}{l}$$
$$v=\frac{eV}{kl}$$
になります。
これを \(I=envS\) に代入すると
$$I=\frac{e^2nS}{kl}V$$
ここで
$$\frac{kl}{e^2nS}=R$$
とおくと
$$IR=V$$
はい。オームの法則が導かれました。
ジュール熱
ジュールの法則を紹介します。
抵抗に電圧を加え、電流が流れるとき熱が発生します。
その熱をジュール熱と呼びます。
ジュール熱を \(Q\) で表すと
$$Q=VIt=RIt^2=\frac{V^2}{R}t$$
ここで出てきた \(t\) は電流を流した時間です。単位はもちろん [s] です。
キルヒホッフの法則
キルヒホッフの法則は2つあります。
先に紹介しますと
第1法則:回路中の任意の分岐点に流れ込む電流の総和と流れ出る電流の総和は等しい
第2法則:回路中の任意の閉じた経路に沿って1周するとき、電池の起電力の総和は抵抗による電圧降下の総和に等しい
というものです。
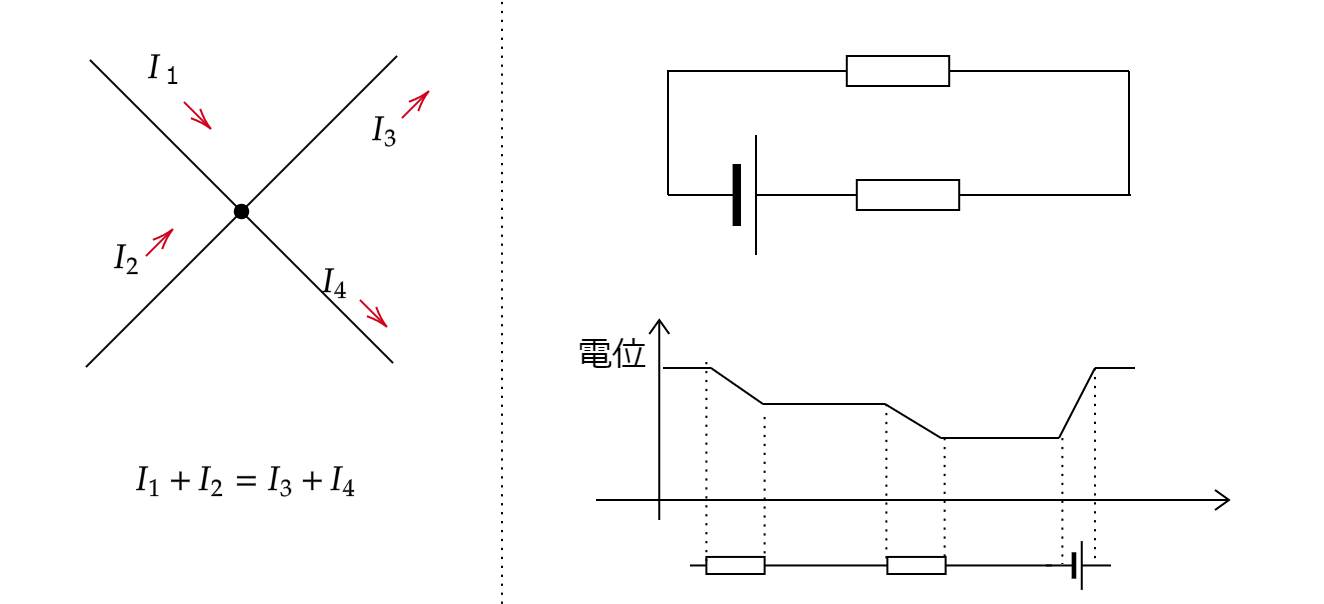
第1法則は図で確認すれば一発です。
上図の左側において、中央の点に入る電流と出ていく電流が
$$I_1+I_2=I_3+I_4$$
第2法則はグラフを確認しましょう。
特に第2法則は言葉だけではわかりにくいので問題を解いてください。
まとめ
今回は電子の運動について見ていきました。
冒頭でも書きましたが、ここから電子の運動を考えることが非常に重要になってきます。
しっかりマスターしましょう!