今回はコンデンサーについて説明します。
電子基板などに搭載されているコンデンサーですがその役割は知っていますでしょうか?
コンデンサについて
コンデンサについて
コンデンサの特徴を挙げると以下の3つが重要です。
- 充電と放電が瞬時にできる
- 直流は通さないが交流は通す
- 周波数が高いほど通しやすい
コンデンサは電気をためることができるもの。という認識で最初は大丈夫です。
コンデンサの説明
まずは真空中の電気容量(どのくらい電気を蓄えられるか)は以下の式で表されます。
$$C_0=\epsilon_0 \frac{S}{d}$$
ここで \(S\) はコンデンサの金属板の面積、\(d\) は2枚の金属板の距離、\(\epsilon\) は真空の誘電率です。
式から金属板の面積が大きくなればなるほど電気をたくさん蓄えられますね。逆に2枚の金属板の距離が開けば開くほど電気容量は小さくなることが分かります。
真空の誘電率は値が決まっています。
もし、金属板の間に物質が挟まっているときは次のようになります。
$$C_0=\epsilon_0\epsilon_r \frac{S}{d}$$
新しく出てきた \(\epsilon_r\) は物質の誘電率でして、物質によって決まっています。
(この電気容量の式はガウスの法則から導くことができます。)
コンデンサの電気容量を用いた式としてこちらも紹介しておきます。
$$Q=CV$$
これは電荷 \(Q\)、電位差 \(V\) を用いた式です。
シンプルではありますが受験物理ではよく見かけます。
直列と並列つなぎ
抵抗は直列につなぐと
$$R_{all}=R_1+R_2+ … +R_n$$
で表されました。
しかしコンデンサは違います。コンデンサを直列につなぐと
$$\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+ … +\frac{1}{C_n}$$
のようになります。
並列につないだ場合は逆です。
コンデンサの合成電気容量は
$$C_{all}=C_1+C_2+ … +C_n$$
になります。
誘電体を挿入するときの変化
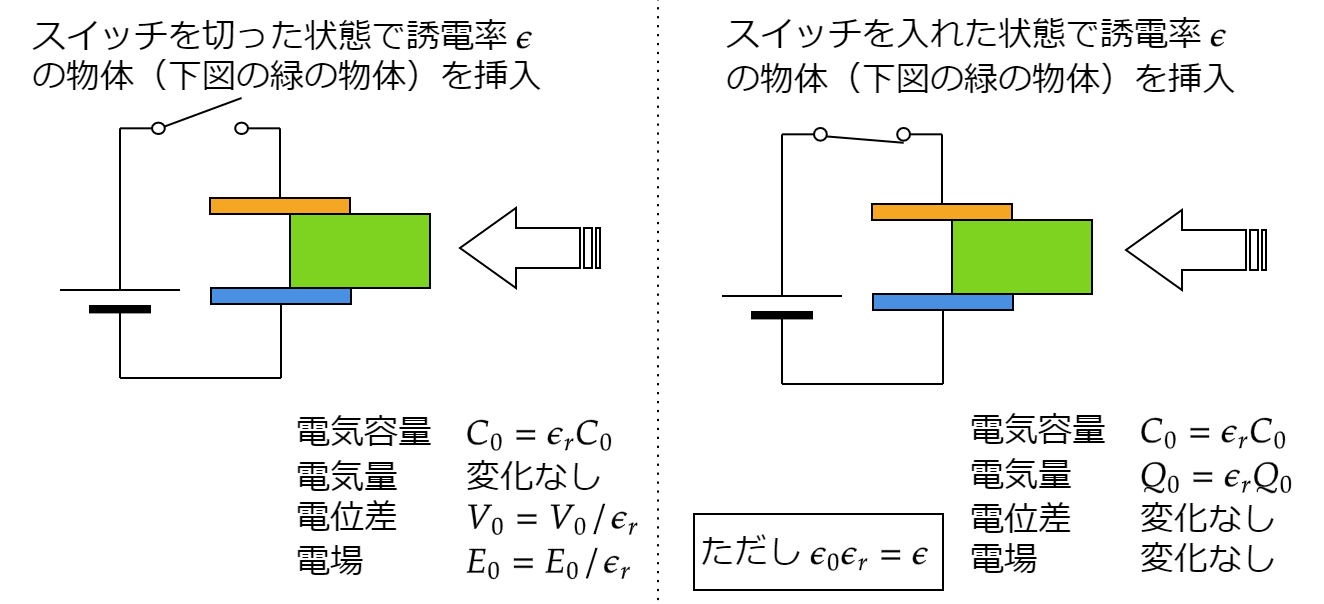
コンデンサーに誘電体を入れた時の様子を見てみましょう
下の図の左側、スイッチを切った状態で誘電体を入れた時はまず、
電気量 Q が一定です。
スイッチが切れている=電源につながっていないので電荷は増えません。そのため Q は一定です。
その他の電気容量、電位差、電場は値が変わります。
\(\epsilon_r >1\)ですので電気容量は 大きくなります。
Q=CVより電位差 V は下がります。(Cは一定ですよ!)
そして V=Ed より電場 E も小さくなります。(dはコンデンサの金属板であるオレンジと青の距離)
今度はスイッチを入れた状態を見ていきましょう。
電気容量は同様に変化します。
しかし電源につながっているので電位差は変わりません。
それに加えて電場も変化しません。
Q=CV より電気量 Q も電気容量と同じように変化します。
静電エネルギー
ここでもエネルギーについて考えます。
コンデンサーに電池を接続して、電荷が蓄えられるとき、コンデンサーには次のようなエネルギーが蓄えられます
$$U=\frac{1}{2}QV=\frac{1}{2}CV^2=\frac{Q^2}{C}$$
これを静電エネルギーといいます。
まとめ
今回はコンデンサーを中心に見ていきました。
入試に計算問題が良く出ますで演習を通して解き方を身につけましょう!