ここでは電場と電位について扱います。
紛らわしい用語が増え、似たような数式が多く存在します。
用語集
しっかり覚えましょう!
| 用語 | 説明 | 点電荷が作る式 |
| クーロンの法則 | 2つの点電荷に働く静電気力はそれぞれの電気量の積に比例し、点電荷の距離の二乗に反比例する | \(F=k_0\frac{qQ}{r^2}\) |
| 電場 | 電荷が空間に及ぼす力 | \(F=k_0\frac{q}{r^2}\) |
| ガウスの法則 | 任意の閉曲面を貫く電気力戦の本数 \(N\) は、閉曲面中にある電荷の総和 \(Q\)に比例する | \(N=4\pi k_0Q\) |
| 電位 | 電荷が持つ静電気力によるエネルギー | \(V=k_0\frac{q}{r}\) |
| 電位差 | 2つの場所の電位の差のこと | \(V_{AB}=V_B-V_A\) |
クーロンの法則
まずはクーロンの法則について学びましょう。
クーロンの法則とは「2つの点電荷(大きさが無視できる電荷)に働く静電気力は、それぞれの電気量の積に比例し、さらに点電荷の距離の二乗に反比例する」
というものです。式を出すとこんな感じです。
$$F=k_0\frac{qQ}{r^2}$$
ここで出てきた \(k_0\) は
$$k_0=\frac{1}{4\pi \epsilon_0}$$
で表されます。さらに、ここで出てきた「\(\epsilon_0\)」は「イプシロン・ゼロ」とよみ、真空の誘電率を意味します。
誘電率とは誘電分極の起こりやすさを表す値でその大きさは
$$\epsilon_0=8.854 187 8123(13)\times 10^{-12} F/m$$
です。
\(q , Q\)は点電荷がもつ電気量で、単位はクーロン、分母にある \(r\) は2つの点電荷間の距離です。
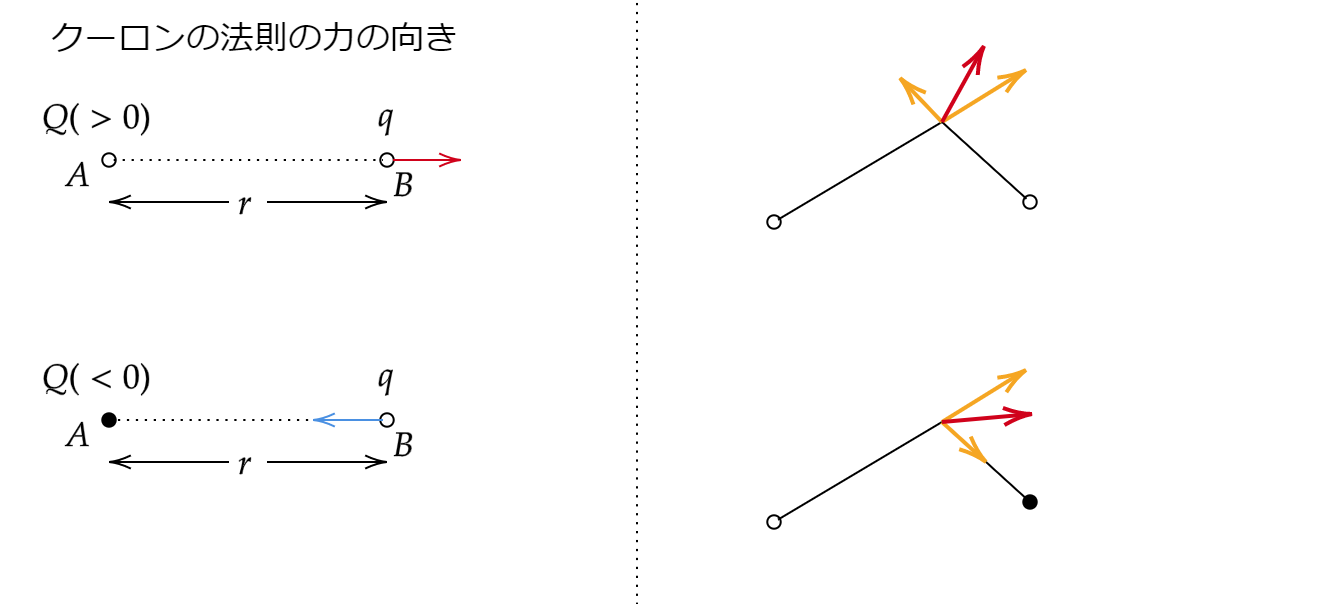
力はベクトルであるので向きを考えましょう。
2つの点電荷の符号が同じであった場合、お互いが反発しあい、斥力(せきりょく)が働きます。
一方2つの点電荷の符号が異なった場合、お互いが引き寄せあり、引力が働きます。
電場とは
静電気力と電場の関係
電荷 \(q\) が空間に存在するとその周囲に電場 \(E\) が生じます。
そこに電荷 \(Q\) を置くと、電荷は電場から静電気力を受けます。
この静電気力Fは電場の強さに比例します。ということで
$$F=qE$$
単位を書くと「静電気力 \(F\)[N] = 電荷 \(q\)[C]×電場 \(E\)[N/C]」です。
点電荷が作る電場は以下の式で表されます。
$$E=k_0\frac{q}{r^2}$$
この電場には向きがあります。それは(のちに説明する)電位の高い方から低い方へ向かう向きになります。
クーロンの法則と一緒に覚えましょう!
ガウスの法則
任意の閉曲面(閉じた曲面)を貫く電気力戦の本数 \(N\) は、閉曲面中にある電荷の総和を \(Q\) とするとき
$$N=4\pi k_o Q$$
になります。これをガウスの法則といいます。詳しくは大学で学ぶので楽しみにしてください。
電位とは
電位
電荷が持つ静電気力による位置エネルギーを電位 \(V\)[V]と呼びます。
静電気力による位置エネルギーUを用いると、電位 \(V\)[V]は
$$U=qV$$
で表されます。
電位差とはその名の通り2つの場所の電位の差を表します。つまり
$$V_{AB}=V_A-V_B$$
です。さらにややこしいことに電位差は「電圧」ともよばれます。
この電圧という用語は電池に使われていますね。
点電荷の周りの電位
点電荷の周りの電位は無限遠を基準(0V)とすると
$$V=k_0\frac{q}{r}$$
で表されます。
まとめ
ややこしくなってきたので表にしてまとめましょう。今回はすべて点電荷が作る○○について学びました。
静電気力(クーロンの法則) \(F=k_0\frac{qQ}{r^2}\)
電場 \(E=k_0\frac{q}{r^2}\)
電位 \(V=k_0\frac{qQ}{r}\)
よって
1.電場と電位の関係は
$$k_0\frac{q}{r}=r\times k_0\frac{q}{r^2}$$
よって
$$V=Ed$$
(今まで2点間の距離を r で表していましたが、慣習的に d で表しました。)
2.静電気力と電場の関係
$$k_0\frac{qQ}{r^2}=Q\times k_0\frac{q}{r^2}$$
よって
$$F=qE$$
しっかり区別して覚えましょう!