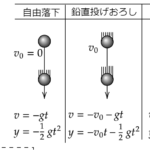
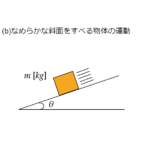
高校物理で最初に学ぶ分野は力学です。
力学は物理の中でも最も基本的な分野の一つであると考えられ、あとで学ぶ電磁気や原子分野でも力学に出てきた公式を使うことがあります。
今回はその中でも速度と加速度を中心に見ていきましょう。
必須用語
まずはこの3つの言葉を覚えましょう!
| 名前 | 記号 | 単位 | 説明 |
|---|---|---|---|
| 変位 | x | [m] | 位置の変化量 |
| 速度 | v | [m/s] | 単位時間あたりに移動する距離を速さといい、速さをベクトル表記した物理量が速度 |
| 加速度 | a | [m/s^2] | 単位時間当たりの速度の変化 |
もう少し詳しく説明していきます。
まずxですが、「位置」として使う場合と「変位」として使う場合の2通りがあります。どちらもベクトルで、「位置」、主に原点からの位置を表します。
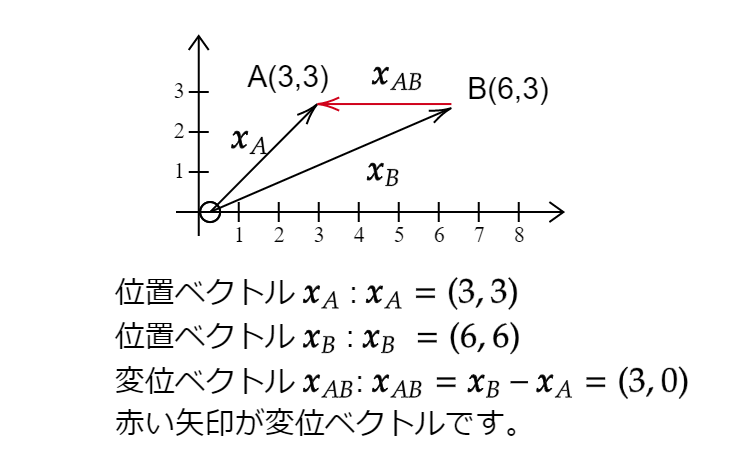
一方「変位」はその名の通り「位置」の変化量です。「変位」を数式で表すと
$$\Delta x=x_A-x_B$$
となります。図で確認します。
等速直線運動の必須公式3つ!
以下は力学を学ぶうえで必須の公式ですので、使いこなせるようにしましょう。
とりあえず羅列してみるとこんな感じです。
$$\vec{x}=\vec{v}_0t+\frac{1}{2}\vec{a}t^2\tag{1}$$
$$\vec{v}=\vec{v}_0+\vec{a}t\tag{2}$$
$$v^2-v_0^2=2ax\tag{3}$$
ただし \(x\) 軸上で考えた場合です。
全てに含まれている \(\vec{v}_0\) は初期速度と呼ばれ、\(t=0\) の時の速度を示しています。
もし、\(t=0\) のときに物体が静止していたら、動いていないので \(\vec{v}_0=0\) となります。
このことはよく覚えておいてください。
物体が止まっているときは速度はゼロです。
ちなみに数学2で学ぶ積分の知識があるのなら(2)を微分してみてください。
変位\(\vec{x}\)を積分すると、速度\(\vec{v}\)になるはずです。
実は(3)式は(1)と(2)から導くことができます。
では、導出してみましょう。
$$\vec{x}=\vec{v}_0t+\frac{1}{2}\vec{a}t^2\tag{1}$$
(1)式を平方完成してください(平方完成は数学1の二次関数の分野で出てきます!)
$$\vec{x}=\frac{1}{2}\vec{a}(t+\frac{\vec{v}_0}{\vec{a}})^2-\frac{\vec{v}_0^2}{2\vec{a}}\tag{4}$$
そして(2)を次のように変形します。
$$\vec{v}=\vec{v}_0+\vec{a}t\tag{2}$$
$$t=\frac{\vec{v}-\vec{v}_0}{\vec{a}}\tag{5}$$
(4)式のtに(5)式を代入します
$$\vec{x}=\frac{1}{2}\vec{a}(\frac{\vec{v}-\vec{v}_0}{\vec{a}}+\frac{\vec{v}_0}{\vec{a}})^2-\frac{\vec{v}_0^2}{2\vec{a}}\tag{6}$$
$$\vec{x}=\frac{1}{2}(\frac{\vec{v}^2}{\vec{a}})-\frac{\vec{v}_0^2}{2\vec{a}}\tag{7}$$
最後に両辺に2aをかければ
$$2\vec{a}\cdot\vec{x}=\vec{v}^2-\vec{v}_0^2\tag{8}$$
(3) 式になりました!
この式の特徴は何といっても時間tを含まないことです。
問題文を読んでも時間が分からないのに、加速度 \(\vec{a}\) や初期速度 \(\vec{v}_0\) を求めなければいけないときは、是非この (3) 式を思い出してほしいです。
これらの式はごちゃごちゃになりやすいのですが、正確に覚えておきましょう。
これらの公式の使い方は?
実は物理に出てくる公式はそこまで多くはない(と思います)。
物理において重要なことは公式の意味と使い方です。
この数式は何を意味しているのか?どのような場面に適してるのか?を考えながら問題を解くと理解が進むはずです。
$$\vec{x}= \vec{v}_0t+\frac{1}{2} \vec{a}t^2\tag{1}$$
例えばこちらの(1)式は変数が4つも入っているのでそのままでは使いにくいです。
大抵の場合は初速度がゼロで右辺の第一項が落ちます。
そして運動方程式(後にでてくる力学で最も重要な式)と組み合わせる問題がよく出てきますので覚えておいてください。
$$ \vec{v}= \vec{v}_0+ \vec{a}t\tag{2}$$
こちらの(2)式はシンプルですね。こちらも初速度がゼロで右辺の第一項が落ちることが多いです。
速度がわかっていて、加速度を求めたいとき、またその逆のパターンとしてよく出てきます。
$$v^2- v_0^2=2ax\tag{3}$$
(3)式については先ほども書きましたが、時間 t を含まないことが特徴です。
問題文を見ても時間に関する情報が与えられていない場合はかなり多いです。
その状態から速度や変位を導けと言われたらこの式の出番です。
ちなみにこの式の左辺はどちらも二乗になっているので全体としてスカラーです。ベクトルでないので気をつけてください。
まとめ
今回は物理学の入門である変位や加速度について学びました。
物理学の中でも力学は重要で、多くの受験生はこの分野を得意としています。
点が取れるようにしっかりと勉強しましょう!
次はこちら!