前回はこちら!3-2重ね合わせの原理・波の反射・干渉
ここでは音の伝わり方と物体の固有振動について勉強します。
用語集
| 用語 | 説明 |
| 音 | 音は三要素(大きさ。高さ。音色)から成り立ちます。狭義的には空気中に伝播する波のこと |
| うなり | 振動数のわずかに異なる音を2つ同時に鳴らした時に起きる現象のこと |
| 固有振動数 | 物体が持っている振動数で、一番振動しやすい値のこと |
| 共振・共鳴 | 振動する物体が外部の振動に反応してより大きく振動すること |
今回は覚える用語が少ないですね。
音の伝わり方
音の正体は波です。
音がどのくらい速いのご存知でしょうか?
音速は約 340 m/s ですので、そんなに速くない(?)です
そんな音の速さ \(V\) は温度に依存しており、以下の式で表せます。
$$V=331.5+0.6t$$
これは空気中の音波の速さを表しており、媒質が変われば音速も変わります。
例として25℃の水中では約1500[m/s]くらいの速さになります。
一応単位に気を付けてください。
上式では単位が秒速[m/s]です。
一般的に車やボールの速さを表すときは時速[km/h]を使っています。
うなり
振動数が少しだけ異なる2つのおんさを同時に鳴らしたときに「うなり」が発生します。
うなりは(言葉で表現しづらいのですが)「うぉーん うぉーん」と聞こえます。
さて、1秒当たりのうなりの振動数 \(f\) は
$$f=|f_1-f_2|$$
で表されます。シンプルですね。
\(f_1\)、\(f_2\) はそれぞれ音源1,2の振動数です。
固有振動数
太鼓は誰が叩いても同じ振動をし、ギターは弦をはじけば毎回同じ振動をします。このようにその物体に固有の振動数で振動することを固有振動といいます。
弦を伝わる波の速さ
弦を伝わる波の速さ \(v\) は弦の張力 \(S\) 、線密度 \(\rho\) を使うと次のようにあらわされます。
$$v=\sqrt{\frac{S}{\rho}}$$
で表せます。振動数はこちらになります
$$f_m=\frac{m}{2l}\sqrt{\frac{S}{\rho}}$$
ただし \(m=1,2,3,…\) です。「振動数×波長=速さ」ですのでこのようになりました。
この式忘れやすい(影が薄い)ので気を付けてください…
頻出ではありませんが、たまに出るので気を付けでください。
閉管
片側が閉ざされている管に波長 \(\lambda\) の波が入ったときの振動条件を見ていきます。
閉館の底までの長さ\(l\) が下の図のように波長の4分の1の奇数倍になれば振動します。
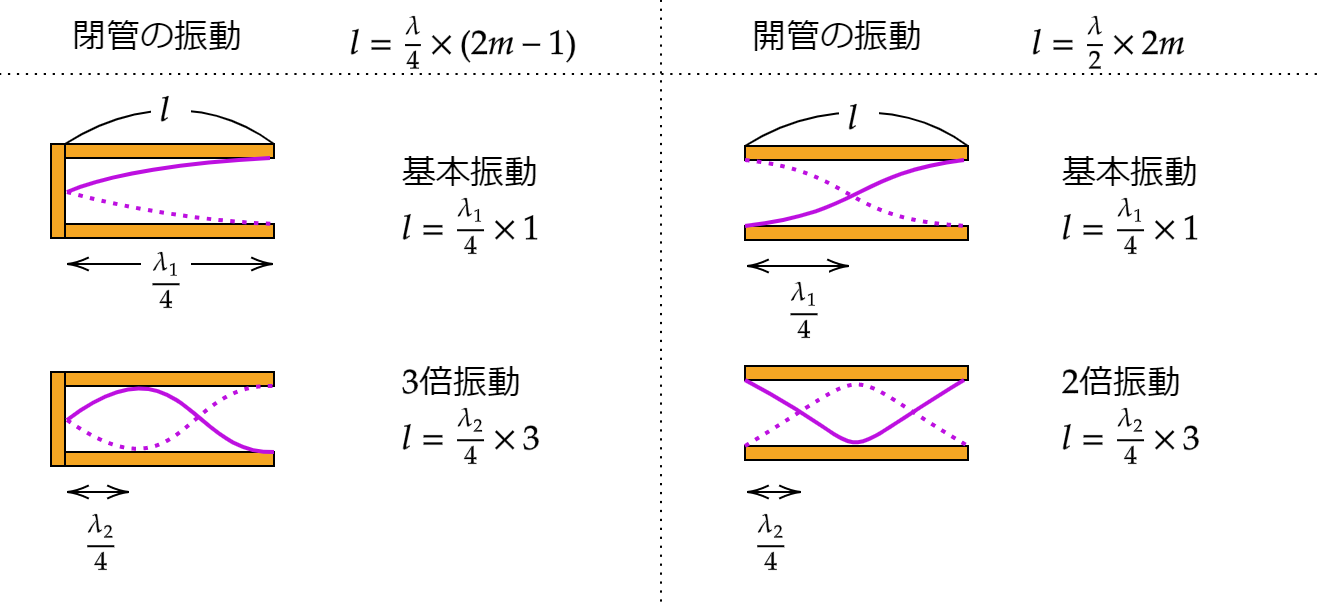
開管
開管の場合の考え方は閉管とほぼ一緒です。
開管では管の長さ \(l\) が波長の2分の1の整数倍になれば振動します。
共振・共鳴
物体がその固有振動数に等しい振動数の周期的な力を受けると大きく振動します。これを共振といいます。
知識として覚えてください。なお、有名な例を挙げるとワシントン州にあるタコマ橋の崩壊があります。是非調べてみてください。
まとめ
今回は音について学びました。
弦を伝わる波の速さの式は忘れやすいので覚えなおしましょう!
次はこちら!3-4ドップラー効果