今回はドップラー効果について説明していきます。
複数の式が出てきますがひとつひとつ覚えるのではなくて、現象そのものを理解すると楽になります!
ドップラー効果の基礎
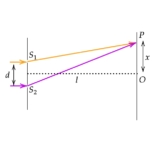
音源の振動数を \(f\) 、速度を \(v_s\) 、音の速さを \(V\) とします。
観測者が観測する音波の振動数 \(f’\) 、波長を \(\lambda’\)とします。
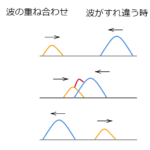
まず知っておいて欲しい事実としてこちらを見てください。
振動数が大きいほど、音が高くなります。
もちろんその逆も成り立ちまして、振動数が小さい=音が低いということになります。
これを頭に入れてドップラー効果を学びましょう!
ドップラー効果とは観測者と波の発生源の相対的な速度の存在によって聞こえてくる音と物体の振動数が異なって聞こえる現象のことを指します。
簡単に説明しますと、人間(もしくはスピーカー)が移動しているとき「スピーカー」が出している音と、「人間が聞く音」の高さに差が出てしまう現象のことです。
止まっている自分の方に「近づいてくる救急車」と、通り過ぎて自分から「遠ざかっていく救急車」の音を聞くと、近づいてくるときは高いのに遠ざかるときは音が低くなります。
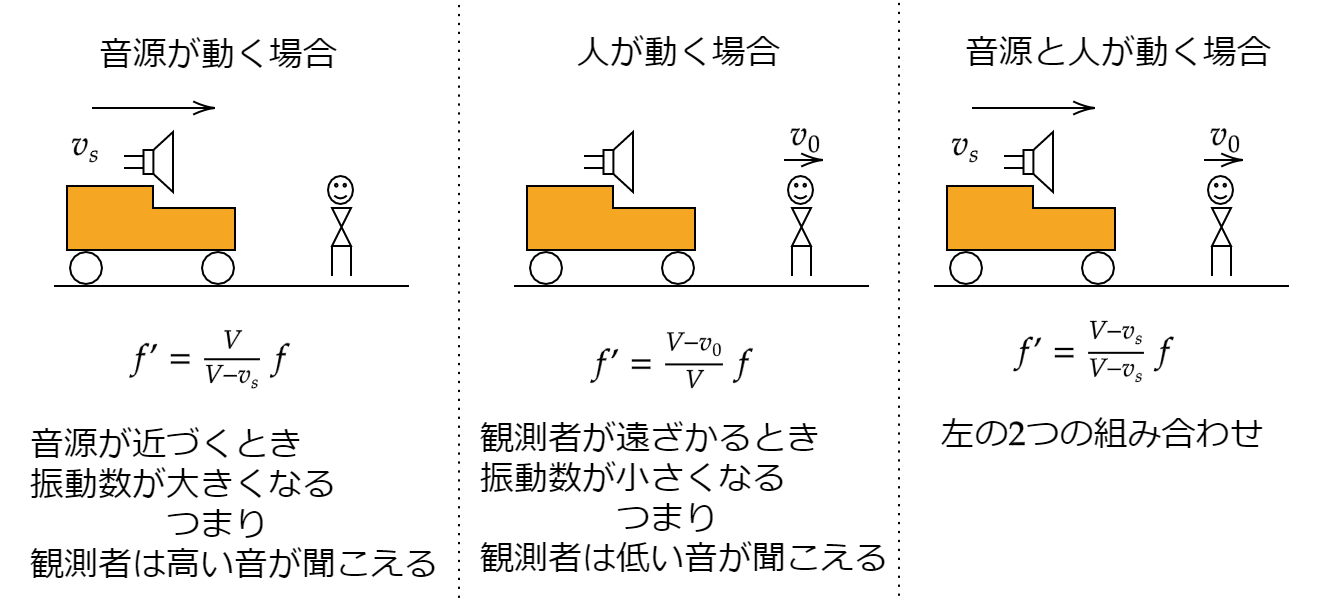
音源が移動する場合
$$f’=\frac{V}{V-v_s}f$$
音源が近づいてくるときの式です。
左辺の \(f’\) は観測者(人間)に聞こえる音の振動数(音の高さ)です。
\(V\) は音源(音を出す物体、救急車など)の速度、\(f\) はその音源の振動数です。
観測者から遠ざかるときは分母にある速度 \(v_s\) がプラスになります。
音源が速く移動して近づいてくるとき、つまり \(v_s\) が大きくなるときは、式に代入してみればわかるとおり観測者に聞こえる振動数 \(f’\) は大きくなります。
人が移動する場合
$$f’=\frac{V-v_0}{V}f$$
これは音源が止まっているときに、観測者が音源から遠ざかるときの振動数を表しています。
観測者が音源に近づくときには \(v_0\) がプラスになります。
プラスにすればよいのかマイナスにすればよいのか迷ったときには次のように考えてください。
音源と観測者の距離が短くなっているときは音が高く(振動数が大きく)なります。
逆に音源と観測者の距離が長くなるときは音が低く(振動数が小さく)なります。
これを頭に入れておけばマイナスにすべきなのかプラスにすべきなのかを判断することができます。
音源と人の両方が移動する場合
$$f’=\frac{V-v_0}{V-v_s}f$$
音源も観測者も動く場合の振動数です。
上の2つを合わせただけになりますので、そこまで難しく考える必要はないです。
反射板が移動する場合
音源と観測者とは別に反射板が出てくるケースがあります。
反射板とは波を反射する板のことです。
これは2つのステップに分ければ解くことができます。
1.音源が反射板に届くときの振動数を \(f’=\frac{V-v_0}{V-v_m}f\) より求める。
2.反射板から振動数 \(f’\) の波が出てくると考え、観測者に音が届くときの振動数 \(f”\)を \(f”=\frac{V-v_m}{V-v_s}f’\) より求める。
です。要は同じような計算を2回行えばよいだけです。
初見でみたときは混乱しますが、落ち着いて計算すれば解くことができます。
進行方向(正負の向き)に注意しましょう!
まとめ
ドップラー効果の問題は波動分野の定番です。
最初は慣れないかと思いますが難しく考える必要はありません。
是非問題演習を繰り返してマスターしましょう!
次はこちら!3-5 光の性質