前回はこちら!1-6エネルギー
今回は運動量と力積について説明します。
これらは前回学んだエネルギーと絡めて出題してくることがあります。
常に速度の向きを考えながら問題を解きましょう!
用語集
漢字が多いのですがしっかり覚えましょう!
| 用語 | 説明 |
| 運動量 | 質量と速度の積。運動の激しさを表す量 |
| 力積 | \(mv_1-mv_2=F\Delta t\) \(F\Delta t\)を力積と呼ぶ |
| 撃力 | 極めて短い時間に働く大きな力のこと |
| 物体系 | 注目する物体のグループ |
| 運動量保存の法則 | 物体系が外力を受けなければこれらの物体の運動量の総和が変化しない |
| 反発係数 | 物体と物体との間の跳ね返り度合い。値が1に近かければよく跳ねる |
| 弾性衝突 | 反発係数が1のときの衝突。力学的エネルギーが保存される |
計算はできるけど用語を覚えていない人は多いのではないでしょうか?
直接入試に出ることはないと思いますが、物理を理解するためにしっかり覚えてください!
運動量と力積
運動量
運動量という言葉を覚えましょう。定義は \(m\vec{v}\) です。
これは運動の激しさを表す量です。質量が大きいもしくは速度が大きい物体の運動が激しいということですね。
単位はそのままでキログラムメートル毎秒[kg・m/s]です。
力積
力積は「力×力が加わった時間」で定義されます。
$$mv_1-mv_2=F\Delta t\tag{1}$$
左辺は上で出てきた「運動量」の変化量です。単位はニュートン秒です。[N・s]
簡単に導出します。
速さの変化量は
$$v_2-v_1=a\Delta t\tag{2}$$
$$a=\frac{v_2-v_1}{\Delta t}\tag{3}$$
となります。これを運動方程式に代入すると
$$m\frac{v_2-v_1}{\Delta t}=F\tag{4}$$
$$mv_2-mv_1=F\Delta t\tag{5}$$
となります。
運動量保存の法則
運動量保存の法則とは
「いくつかの物体が内力を及ぼしあうだけで、外力を受けないとき物体系の運動量の総和は変化しない。」
というものです。
もう少しわかりやすく言うと
「物体系に外からの力が働かないとき、衝突前の運動量の合計=衝突後の運動量の合計」
です。ちなみに外力とは注目している物体系以外から働く力のことです。
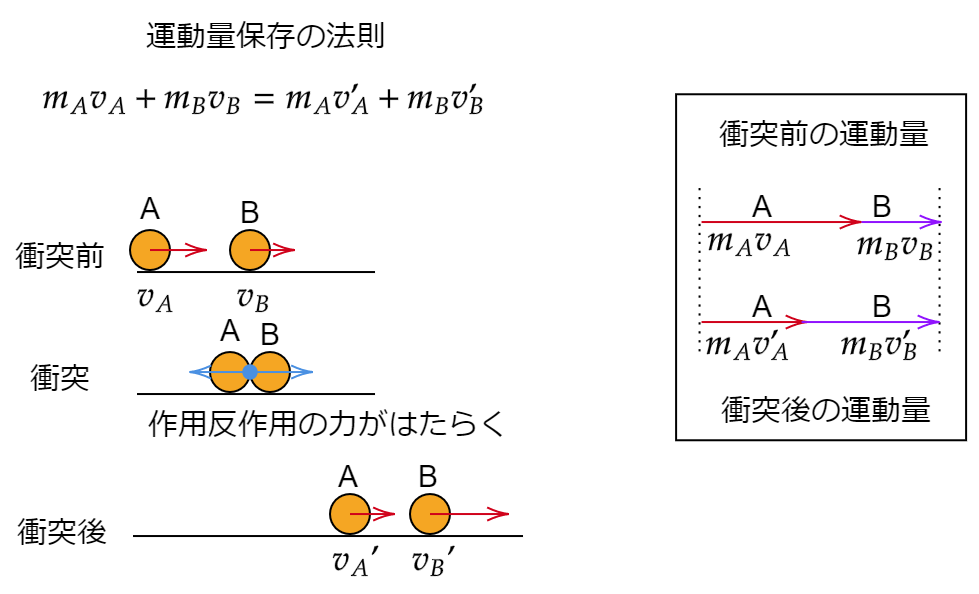
衝突するときには作用反作用の力が働きます。作用反作用は2つの物体間に働く大きさが同じで、向きが真逆の力のことでしたね。
直線上での衝突以外にもこの運動量保存則は成り立ちます。
そんなときは力の成分を水平方向と鉛直方向に分けて考えましょう!
反発係数と弾性衝突
床との衝突の場合
反発係数とは「小球(物体)と床の材質によって決まる、跳ね返りの度合い」を表す物理量で、大きさは(\(0 \leq e \leq 1\))で表されます。
反発係数が1のときを弾性衝突といいます。
逆に1でないときは非弾性衝突と呼ばれ、特にeが0のときを完全非弾性衝突と呼ばれます。
さて、反発係数の式はこのように表されます。
$$e=|\frac{v’}{v}|\tag{6}$$
「反発後の速度÷衝突前の速度」で定義されます。
反発係数eが1以下であるため、床に衝突して加速されるということはありません。
これは定義を覚えれば簡単です。では次に2つの物体の衝突のケースを見ていきます。
2つの物体の衝突
今度は、2つの物体間での衝突の場合を見ていきます。定義はこちらです。
$$e=\frac{|v_1′-v_2’|}{|v_1-v_2|}\tag{7}$$
\(「’」は衝突後の速度を表しています\)
日本語で説明すると
「衝突後の2つの物体の速度の差÷衝突前の2つの物体の速度の差=反発係数」です。
「速さ」ではなく「速度」ですので向きを気にしてください!
(速さは大きさだけを持つ「スカラー」であり、速度は大きさと向きを持つ「ベクトル」です。)
問題
以下の問題を解いてみましょう。
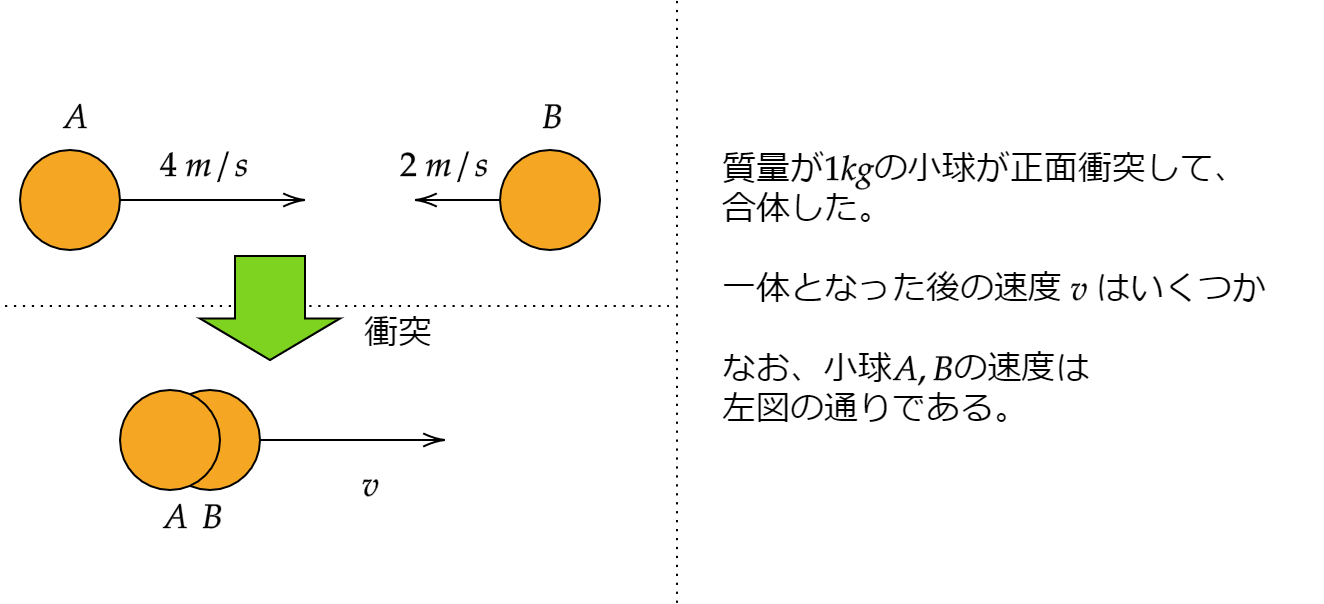
はい。では答えです。
右側を正とします。
$$mv_2+mv_1=mv+mv$$
\(m\) は質量で今回は1kgです。
$$v_2+v_1=2v$$
$$4-2=2v$$
$$v=1$$
ということで右向きに1m/sの速さが答えになります。
まとめ
今回は運動量について学びました。
ここでは向きが重要です。物体は常にどっちに動いているのかを気にしながら問題を解きましょう!
次回はこちら!1-8円運動