今回は高校力学分野に出てくる公式と用語を載せました。
復習用に使ってください!
公式集
ではいきます。
| 用語・名前 | 公式 | 説明 |
| 振動数と周期 | $$f=\frac{1}{T}$$ | 振動数 \(f\) は1秒間の振動の回数を表したものです。
周期は \(T\) は媒質が1回の振動に要する時間のことです。 |
| 変位 | $$\Delta x = x_A – x_B$$ | 位置の変化量 |
| 位置 | $$\vec{x}=\vec{v}_0t+\frac{1}{2}\vec{a}t^2$$ | 動いている物体の位置などを求めるときに使用する。 |
| 速度 | $$\vec{v}=\vec{v}_0+\vec{a}t$$ | 動いている物体の速度などを求めるときに使用する。 |
| 加速度 | $$v^2-v_0^2=2ax$$ | 動いている物体の加速度などを求めるときに使用する。 |
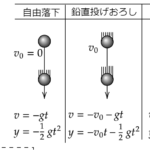
| 自由落下 | $$v=gt, y=\frac{1}{2}gt^2$$ | 物体に加速度を与えず重力だけから力を受けているときの運動 |
| 鉛直投げ下ろし | $$v=v_0+gt, y=v_0t+\frac{1}{2}at^2$$ | 物体に鉛直下方向に加速度を与えたときの運動 |
| 鉛直投げ上げ | $$v=v_0-gt, y=v_0t-\frac{1}{2}at^2$$ | 物体に鉛直上方向に加速度を与えたときの運動 |
| 回転する物体の力のモーメント | $$M=Fl \sin\theta$$ | 回転させる力の大きさを表す量 |
| フックの法則 | $$F=kx $$ | バネを用いたときに物体が受ける力の関係式 |
| バネの合成(直列) | $$\frac{1}{k_{all}}= \frac{1}{k_A}+\frac{1}{k_B}$$ | バネが直列につながっているときのばね定数 |
| バネの合成(並列) | $$k_{all}=k_1+k_2+k_3+\cdots+k_n$$ | バネが並列につながっているときのばね定数 |
| 圧力 | $$pS=F$$ | ある物体の面積に加わる力 |
| 浮力 | $$F=mg=\rho Vg$$ | 物体に加わる重力とは逆方向に加わる力 |
| 運動方程式 | $$m\vec{a}=\vec{F}$$ | 運動方程式は運動方程式です。 |
| 仕事 | $$W=Fx$$ | 単位は[J](ジュール)距離\(\times\)その方向に働いた力 |
| 仕事率 | $$P=W/t$$ | 単位は[W](ワット)単位時間あたりにする仕事。仕事の効率の良さを表す |
| 運動エネルギー | $$K=\frac{1}{2}mv^2$$ | 速さ \(v\) [m/s]の物体が持つエネルギー |
| 位置エネルギー | $$U=mgh$$ | 基準点から高さ \(h\) [m]にある物体が持つエネルギー |
| 弾性エネルギー | $$U=\frac{1}{2}kx^2$$ | ばねなどの伸び縮みする物体が蓄えるエネルギー |
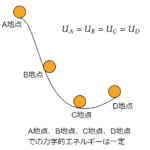
| 力学的エネルギーの保存 | $$U_{total}=K_1+U_1=K_2+U_2$$ | 物体が保存力だけから仕事を受けるときその和が一定 |
| 力積 | $$mv_1-mv_2=F\Delta t\\F\Delta t$$
|
運動量の変化量 |
| 角速度 | $$\omega=\frac{\theta}{t}$$ | 1秒あたりに何度回転するか |
| 遠心力 | $$F=ma=mr\omega^2=m\frac{v^2}{r}$$ | 物体が円運動を行うとき、見かけの上でその物体に働く力のこと |
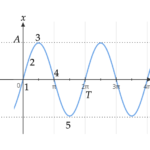
| 単振動 | $$x=A\sin(\omega t+\theta_0)$$ | 等速円運動を横から見たときの上下運動のこと |
| 周期 | $$T=2\pi \sqrt{\frac{l}{g}}$$ | 一定周期ごとに同じ現象が繰り返されるとき、その時間を周期という |
| 万有引力 | $$F=G\frac{m_1m_2}{r^2}$$ | 質量を持つ全ての物体の間に作用する引力のこと |
いかがでしょうか?
思ったより少ないのではないでしょうか?
次は用語を覚えましょう!
用語集
ではいきます。
| 用語 | 説明 |
| 波 | 振動が次々と周りに伝わる現象 |
| 変位 | x[m] 位置の変化量 |
| 速度 | v[m/s] 単位時間あたりに移動する距離を速さといい、速さをベクトル表記した物理量が速度 |
| 加速度 | a[m/s^2] 単位時間当たりの速度の変化 |
| 重力 | 物体に対して常に鉛直下向き(地面の方向)に働く力。 |
| 重力加速度 | 地球の重力が物体におよぼす加速度。
大きさは約9.8m/s^2 |
| 自由落下 | 静止している物体が重力だけを受けて落下する運動のこと |
| 運動の対称性 | 原点を対称に、時間や速度の大きさが一致すること。 |
| 質点(しつてん) | 大きさを無視できる物体 |
| モーメント | 物体の回転させる力の大きさのこと モーメントが大きいとは物体が回転しにくいということ |
| 剛体(ごうたい) | 力を加えても変形しない理想的な物体 |
| 偶力(ぐうりょく) | 同じ大きさで反平行(向きが逆向きで平行)な2つの力 |
| 重心(じゅうしん) | 重力の作用点 |
| ばね定数 | 「k」で表すことが多く、ばねの伸び縮みやすさを表します。値が大きければ伸び縮みしにくいということを意味します |
| 圧力 | 「p」で表すことが多く、単位面積あたりに働く力を意味します |
| 浮力 | 浮く力。物体の上側と下側に加わる圧力の差から生じます |
| 垂直抗力 | 接触している固体を押し返す力です |
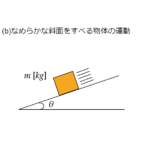
| 粗い面 | 摩擦があるということを意味します(一応覚えてください…) |
| 大気圧 | 地球上の大気(空気)が物体や我々人間に加える圧力のこと |
| 慣性の法則 | 物体が外力を受けない、もしくは外力が釣り合っている限り、静止している物体は静止し続け、運動している物体は等速度運動しつづける |
| 運動方程式 | 力の大きさが物体の質量と加速度に比例する |
| 作用反作用の法則 | 2つの物体間で及ぼしあう力で、一方を作用と呼ぶとき、もう一方を反作用と呼びます。この関係を作用反作用と呼びます |
| 運動量 | 質量と速度の積。運動の激しさを表す量 |
| 撃力 | 極めて短い時間に働く大きな力のこと |
| 物体系 | 注目する物体のグループ |
| 運動量保存の法則 | 物体系が外力を受けなければこれらの物体の運動量の総和が変化しない |
| 反発係数 | 物体と物体との間の跳ね返り度合い。値が1に近かければよく跳ねる |
| 弾性衝突 | 反発係数が1のときの衝突。力学的エネルギーが保存される |
| 円運動 | 円周上を運動することです。ここでは等速円運動を見ていきます |
| 角速度 | 1秒当たりの物体の回転数 |
| 周期 | 円運動している物体が1周するのに必要な時間 |
| 回転数 | 1秒間に回転する数 |
| 向心力 | 等速運動する物体が円の中心に向かってはたらく力 |
| 慣性力 | 観測者が加速度運動していることが原因となって表れる見かけ上の力 |
| 遠心力 | 観測者が物体とともに円運動をするときの慣性力のこと |
| 等速円運動 | 円周上を等速で動く運動 |
| 単振動 | 正弦関数で表される周期運動 |
| 角振動数 \(\omega\)[rad/s] | 回転の速度を表す、角周波数ともいう |
| 周期 \(T\) [s] | 振動が一往復するのに必要な時間 |
| 復元力 \(F\) [N] | 物体がつり合いの位置に戻ろうとするときに働く力 |
| ばね振り子 | ばねに物体を付けて往復運動する装置 |
| 振幅 \(A\) [m] | 振動の大きさ |
| 位相 \(\omega t\) [rad] | 物体がどのような振動状態にあるのかを表す |
| 振動数 \(f\) [Hz] | 1秒間に振動する数 |
| 振り子の等時性 | 振り子の周期が振幅によらず一定であること |
| 位相 | 回転角 |
| 天動説 | 地球を中心として周りの天体が動いていると考えること |
| ケプラーの第一法則 | 惑星は太陽を一つの焦点とする楕円軌道を描く |
| ケプラーの第二法則 | 面積速度一定の法則。惑星と太陽を結ぶ線分が、一定時間に描く面積は一定である |
| ケプラーの第三法則 | 惑星の公転周期の2乗は楕円軌道の半長軸の3乗に比例する |
| 万有引力の法則 | 二つに物体間に働く力はそれぞれの質量の積に比例し、距離の二乗に反比例する |
| 第一宇宙速度 | 地表近くを円軌道を描いて回る物体の速度 |
| 第二宇宙速度 | 地球から飛び去るために必要な最小限の速度 |
| ケプラーの第一法則 | 惑星は太陽を一つの焦点とする楕円運動を描く |
| ケプラーの第二法則 | 面積速度一定の法則 |
| 第一宇宙速度 | 地表近くを円軌道を描いて回る物体の速度のこと |
| 第二宇宙速度 | 地球から飛び去るために必要な最小限の速度のこと |
まとめ
一覧表を作っておいていうのもあれですが、公式は覚えるだけではだめです。
しっかり使えるようにしましょう!