前回はこちら! 1-1 変位と速度と加速度
ここでは「自由落下」「鉛直投げおろし」「鉛直投げ上げ」「水平運動」「放物運動」について取り扱います。
これらの運動は小球(大きさを無視できるような小さいボールのこと)を投げた時の運動について見ていきます。
5つもパターンがあるように見えますが、考え方は同じですので心配しないでください。
5つの落下・放物運動
とりあえずこのページで取り扱う5つの運動を図にしてみました。
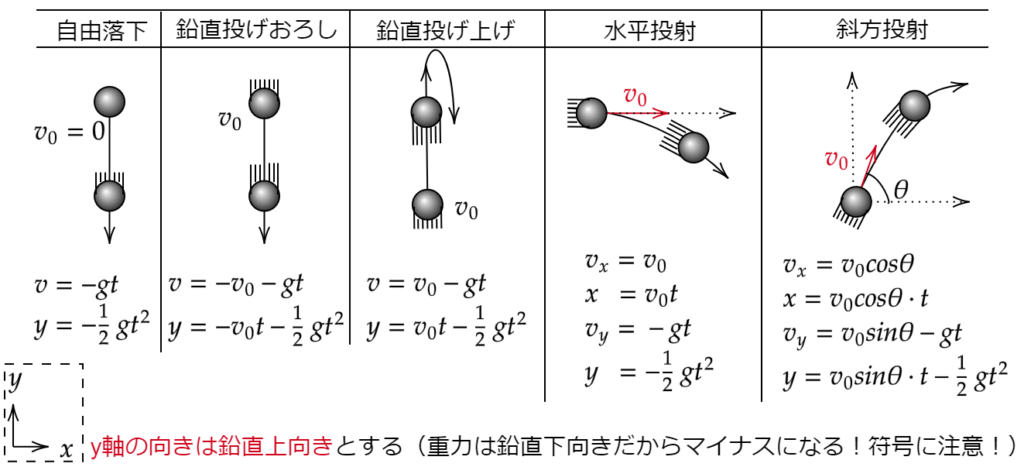
このページで重要なことは
- y軸の向きに気を付ける
- 重力は常に鉛直下向き
- sin と cos の三角関数の基礎知識が必要
です。
放物運動において重要な重力について話します。
重力は常に鉛直下向き(地面の方向)に働く力です。上の式で出てくる \(g\) は重力加速度と呼ばれています。この重力加速度 \(g\) の値は9.8m/s^2とすることが多いです。
(実際地球上の緯度の違いによって値が若干変わります。例えば、北海道の札幌では約9.805m/s^2で、沖縄の那覇では約9.791m/s^2です。これは地球の自転の遠心力の影響を受けているからです。興味があったら調べてみましょう!)
問題文に「重力加速度は9.8m/s^2とする」と書かれていることが多いのですが、問題演習をこなせば自然と覚えられると思います。
自由落下
自由落下について説明します。
自由落下とは静止している物体が重力だけを受けて落下する運動のことを指します。
つまり勢いをつけずにそのまま重力に任せて落下する運動を自由落下というのです。
等加速度運動の式で出てくるこちらの速度の式を覚えていますか?
$$v=at\tag{1}$$
自由落下運動では加速度 \(a\) に重力加速度 \(g\) を代入するだけです。
早速やってみましょう。こんな感じです。
$$v=gt\tag{2}$$
簡単ですよね。位置 \(y\) についても同様で、前回出てきた公式を使って
$$y=\frac{1}{2}gt^2\tag{3}$$
です。(ここでは鉛直運動を考えているため x ではなく y にしました。自分が分かればどっちでも大丈夫です。)
鉛直投げおろし
次は鉛直投げおろし運動です。
これは勢いをつけて鉛直下向き(y軸のマイナス方向、地面の方向)に小球を投げるだけです。
つまり、先ほどの自由落下運動の式に初期速度 \(v_0\) を付け加えてみると。
$$v=v_0+gt\tag{4}$$
こんな感じですね。位置も同様に
$$y=v_0t+\frac{1}{2}at^2\tag{5}$$
初期速度に時間を掛けた項を足せばOKです。
鉛直投げ上げ
鉛直投げ上げ(y軸の正の方向、空の方向)運動は以下の図で表せます。
基本的に地球上では重力が働くため、上に投げ上げられた物体は徐々に減速し、最終的には落ちてきます。
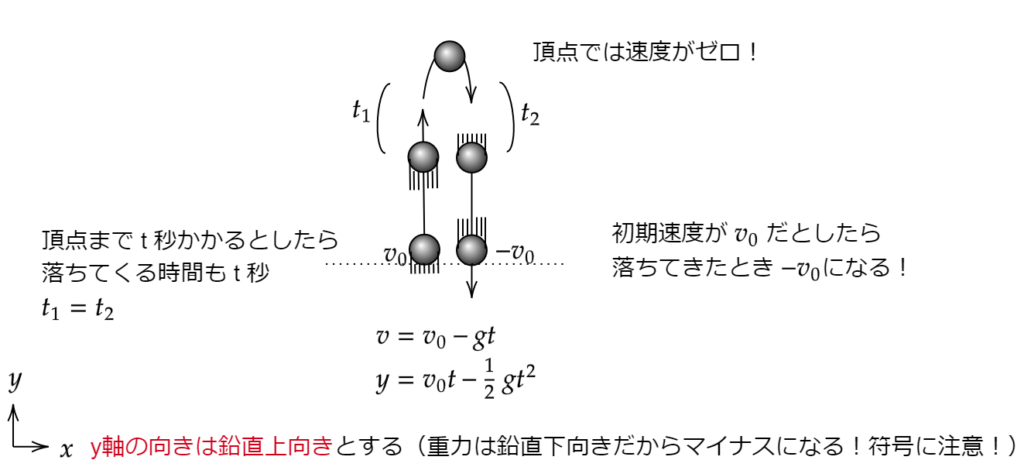
\(t_2\)は頂点から投げた位置まで落ちてくる時間
本来ならば同じ場所に落ちてくるが、ここでは見やすさのため横にずらして書いてある
ここで注意してほしい点、問題としてよく出される点を説明していきます。
その1、頂点では速度がゼロ
ほんの一瞬ですが頂点では静止します。静止する=速度がゼロということになります。
この性質は問題を解くときによく出てくるので覚えてください。
その2、投げ上げた物体が頂点に達するまでにかかる時間 \(t_1\) と、頂点から投げ上げたところと同じ高さまで落ちてくるときにかかる時間 \(t_2\) は同じです。
式で表すと \(t_1=t_2\) が成り立ちます。
これを運動の対称性といいます。
つまりボールを真上に投げて、最高点に達するまでの時間が5秒だったとしましょう。
そのボールが落ちて自分に当たるまでの時間も同じく5秒かかるということです。
(なお、速度は大きさが同じで向きが逆方向になります。)
これらの知識は斜方投射でも役に立ちますので覚えてください。
水平投射
水平投射とは真横に小球を投げる運動のことです。
水平投射における鉛直方向(y軸方向)の初期速度がゼロですので、自由落下と同様です。
ここで重要なのは横軸方向です。
鉛直方向(y軸方向)は重力が加わるため徐々に速度が上がりますが、水平方向(x軸方向)に重力は存在しません。
ほとんどの入試問題では空気抵抗などを無視するため、水平方向(x軸方向)の速度は常に初期速度 \(v_0\) で一定です!
鉛直方向は重力加速度が働いているため、速度は変化しますが、水平方向は加速度がゼロですので、速度は変わらないということです。
これは次の斜方投射でも同様です。
斜方投射
斜方(ななめ方向)投射です。ここでは鉛直方向と水平方向に分けて考えることが大事です!
鉛直方向と水平方向に分ければ、先へ℃勉強した、鉛直投げ上げや水平投射に帰結しますよね。
斜め上に投げているときは
(x軸方向は水平投射)+(y軸方向は鉛直投げ上げ)
斜め下に投げているときは
(x軸方向は水平投射)+(y軸方向は鉛直投げおろし)
に分けて考えるだけで大丈夫です。
その際に三角関数の基礎知識が必要になります。
三角関数は数学1と数学2で習うので、基礎レベルの知識がない人はまず物理を勉強する前に数学を勉強するべきだと思います…。
高校物理では専門的な知識を必要としませんが、三角関数や二次関数の計算はたくさん出てくるので気を付けてください。
問題
問題を解いてみましょう。以下の図を見てください。
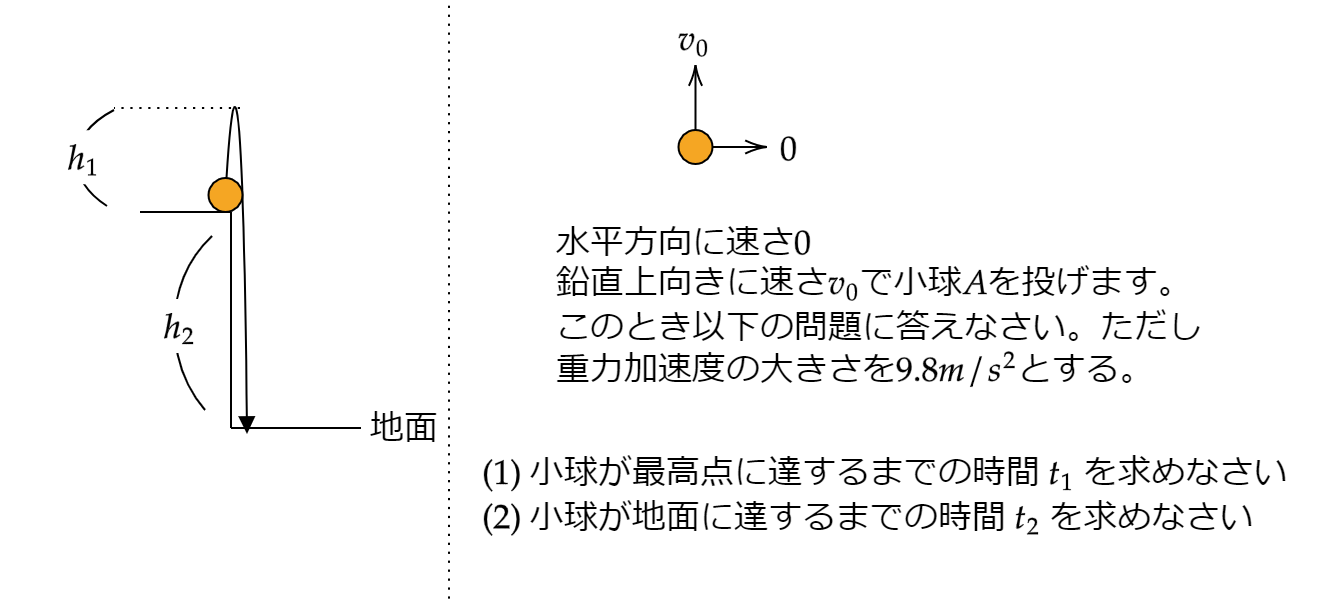
(1)小球が最高点に達するまでの時間 \(t_1\) を求めなさい。の答え
今の状況を考えてみましょう。
これは鉛直投げ上げ運動でして、高さ \(h_1\) と速度 \(v_0\) それに重力加速度が分かっています。
そのため、ここで
$$v=v_0-gt\tag{6}$$
が使えます。
注意してほしい点は \(v_0\) と重力加速度 \(g\) の向きが逆ですので、マイナスが付きます。
そして最高点では速度 \(v\) がゼロになるので
$$0=v_0-gt_1\tag{7}$$
$$v_0=gt_1\tag{8}$$
$$\frac{v_0}{g}=t_1\tag{9}$$
となります。これで(1)の答えが出ました。
(2)小球が地面に達するまでの時間を求めましょう。の答え
最高点までの時間 \(t_1\) は先ほど算出しました。
最高点では速度がゼロになるのでそこからは自由落下運動になります。
ということで
$$y=\frac{1}{2}gt^2\tag{10}$$
小球が最高点から落ちて地面に達するまでの時間を \(t’\) とすると
$$(h_1+h_2)=\frac{1}{2}gt’^2\tag{11}$$
$$\frac{2(h_1+h_2)}{g}=t’^2\tag{12}$$
$$\sqrt{\frac{2(h_1+h_2)}{g}}=t’\tag{13}$$
では最後に \(t_2\) を計算しましょう
$$t_2=t_1+t’\tag{14}$$
$$t_2=\frac{v_0}{g}+\sqrt{\frac{2(h_1+h_2)}{g}}\tag{15}$$
ということになります。
まとめ
最後にもう一度全部を見てみましょう

いろいろあって最初は戸惑いやすいと思いますがよくよく見てみれば結構似ています。
符号に注意して問題を解きまくりましょう!
次はこちら!1-3.剛体に働く力・モーメント